Question

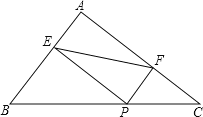
【题目】如图，在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点（且点P不与点B、C重合），PE⊥AB于E，PF⊥AC于F．则EF的最小值为_____

Answer 1

【答案】4.8

【解析】

先由矩形的判定定理推知四边形PEAF是矩形；连接PA，则PA=EF，所以要使EF，即PA最短，只需PA⊥CB即可；然后根据三角形的等积转换即可求得PA的值．

如图，连接PA．

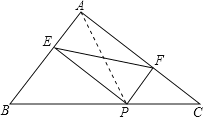
∵在△ABC中，AB=6，AC=8，BC=10，
∴BC2=AB2+AC2，
∴∠A=90°．
又∵PE⊥AB于E，PF⊥AC于F．
∴∠AEP=∠AFP=90°，
∴四边形PEAF是矩形．
∴AP=EF．
∴当PA最小时，EF也最小，
即当AP⊥CB时，PA最小，
∵ABAC= BCAP，即AP= = =4.8，
∴线段EF长的最小值为4.8；

故答案为：4.8