题目内容
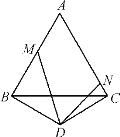
【题目】如图所示,点![]() 是正方形
是正方形![]() 的对角线
的对角线![]() 上一点,
上一点,![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() ,给出下列四个结论:
,给出下列四个结论:
①![]() ;②
;②![]() 一定是等腰三角形;③
一定是等腰三角形;③![]() ;④
;④![]() ,
,
其中正确结论的序号是________.

【答案】①③④
【解析】
连接PC,根据正方形的对角线平分一组对角可得∠ABP=∠CBP=45°,然后利用“边角边”证明△ABP和△CBP全等,根据全等三角形对应边相等可得AP=PC,对应角相等可得∠BAP=∠BCP,再根据矩形的对角线相等可得EF=PC,对边相等可得PF=EC,再判断出△PDF是等腰直角三角形,然后根据等腰直角三角形的斜边等于直角边的![]() 倍解答即可.
倍解答即可.
如图,连接PC,
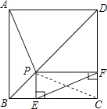
在正方形ABCD中,∠ABP=∠CBP=45°,AB=CB,
∵在△ABP和△CBP中,
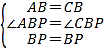
∴△ABP≌△CBP(SAS),
∴AP=PC,∠BAP=∠BCP,
又∵PE⊥BC,PF⊥CD,
∴四边形PECF是矩形,
∴PC=EF,∠BCP=∠PFE,
∴AP=EF,∠PFE=∠BAP,故①③正确;
∵PF⊥CD,∠BDC=45°,
∴△PDF是等腰直角三角形,
∴PD=![]() PF,
PF,
又∵矩形的对边PF=EC,
∴PD=![]() EC,故④正确;
EC,故④正确;
只有点P为BD的中点或PD=AD时,△APD是等腰三角形,故②错误;
综上所述,正确的结论有①③④.
故答案为:①③④.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目