题目内容
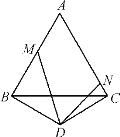
【题目】如图,已知等边三角形△ABC边长为a,等腰三角形△BDC中,∠BDC=120,∠MDN=60,角的两边分别交AB,AC于点M,N,连结MN.则△AMN的周长为( )
A.aB.2aC.3aD.4a
【答案】B
【解析】
根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长AB至F,使BF=CN,连接DF,通过证明△BDF≌△CDN及△DMN≌△DMF,从而得出MN=MF,△AMN的周长等于AB+AC的长.
解:∵△BDC是等腰三角形,且∠BDC=120°
∴∠BCD=∠DBC=30°
∵△ABC是边长为3的等边三角形
∴∠ABC=∠BAC=∠BCA=60°
∴∠DBA=∠DCA=90°
延长AB至F,使BF=CN,连接DF,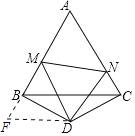
在Rt△BDF和Rt△CND中,BF=CN,DB=DC
∴Rt△BDF≌Rt△CDN(HL),
∴∠BDF=∠CDN,DF=DN
∵∠MDN=60°
∴∠BDM+∠CDN=60°
∴∠BDM+∠BDF=60°,∠FDM=60°=∠MDN,DM为公共边
∴△DMN≌△DMF(SAS),
∴MN=MF
∴△AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=2a,
故选:B.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目




