题目内容
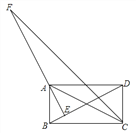
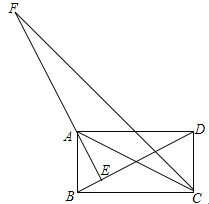
【题目】如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=![]() ;④AF=
;④AF=![]() ,其中正确的是______.(填写所有正确结论的序号)
,其中正确的是______.(填写所有正确结论的序号)
【答案】①③④
【解析】分析:根据余角的性质得到∠BAE=∠ADB,等量代换得到∠BAE=∠CAD,故①正确;根据三角函数的定义得到tan∠DBC=![]() =
=![]() ,于是得到∠DBC≠30°,故②错误;由勾股定理得到BD=
,于是得到∠DBC≠30°,故②错误;由勾股定理得到BD=![]() =2
=2![]() ,根据相似三角形的性质得到AE=
,根据相似三角形的性质得到AE=![]() ;故③正确;根据角平分线的定义得到∠BCF=45°,求得∠ACF=45°﹣∠ACB,推出∠EAC=2∠ACF,根据外角的性质得到∠EAC=∠ACF+∠F,得到∠ACF=∠F,根据等腰三角形的判定得到AF=AC,于是得到AF=2
;故③正确;根据角平分线的定义得到∠BCF=45°,求得∠ACF=45°﹣∠ACB,推出∠EAC=2∠ACF,根据外角的性质得到∠EAC=∠ACF+∠F,得到∠ACF=∠F,根据等腰三角形的判定得到AF=AC,于是得到AF=2![]() ,故④正确.
,故④正确.
详解:在矩形ABCD中,∵∠BAD=90°.∵AE⊥BD,∴∠AED=90°,∴∠ADE+∠DAE=∠DAE+∠BAE=90°,∴∠BAE=∠ADB.∵∠CAD=∠ADB,∴∠BAE=∠CAD,故①正确;
∵BC=4,CD=2,∴tan∠DBC=![]() =
=![]() ,∴∠DBC≠30°,故②错误;
,∴∠DBC≠30°,故②错误;
∵BD=![]() =2
=2![]() .∵AB=CD=2,AD=BC=4.∵△ABE∽△DBA,∴
.∵AB=CD=2,AD=BC=4.∵△ABE∽△DBA,∴![]() ,即
,即![]() ,∴AE=
,∴AE=![]() ;故③正确;
;故③正确;
∵CF平分∠BCD,∴∠BCF=45°,∴∠ACF=45°﹣∠ACB.∵AD∥BC,∴∠DAC=∠BAE=∠ACB,∴∠EAC=90°﹣2∠ACB,∴∠EAC=2∠ACF.∵∠EAC=∠ACF+∠F,∴∠ACF=∠F,∴AF=AC.∵AC=BD=2![]() ,∴AF
,∴AF![]() ,故④正确;
,故④正确;
故答案为:①③④.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】已知![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,
,![]() ;
;
(1)对照数轴填写下表:
| 6 | -1 | -2 | 4 |
| 4 | -5 | 3 | -4 |
|
(2)若![]() 、
、![]() 两点间的距离记为
两点间的距离记为![]() ,试问:
,试问:![]() 和
和![]() ,
,![]() 有何数量关系?
有何数量关系?
(3)写出所有符合条件的整数点![]() ,使它到10和-10的距离之和为span>20,并求所有这些整数的数的和;
,使它到10和-10的距离之和为span>20,并求所有这些整数的数的和;
(4)找出(3)中满足到10和-10的距离之差大于1而小于5的整数的点![]() ;
;
(5)若点![]() 表示的数为
表示的数为![]() ,当点
,当点![]() 在什么位置时,
在什么位置时,![]() 取得的值最小,并求出这个最小值.
取得的值最小,并求出这个最小值.
【题目】如图,在边长为![]() 的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
三角形的直角边长/ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
阴影部分的面积/ | 398 | 392 | 382 | 368 | 350 | 302 | 272 | 200 |

(1)在这个变化过程中,自变量、因变量各是什么?
(2)请将上述表格补充完整;
(3)当等腰直角三角形的直角边长由![]() 增加到
增加到![]() 时,阴影部分的面积是怎样变化的?
时,阴影部分的面积是怎样变化的?
(4)设等腰直角三角形的直角边长为![]() ,图中阴影部分的面积为
,图中阴影部分的面积为![]() ,写出
,写出![]() 与
与![]() 的关系式.
的关系式.