题目内容
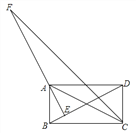
【题目】已知![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,
,![]() ;
;
(1)对照数轴填写下表:
| 6 | -1 | -2 | 4 |
| 4 | -5 | 3 | -4 |
|
(2)若![]() 、
、![]() 两点间的距离记为
两点间的距离记为![]() ,试问:
,试问:![]() 和
和![]() ,
,![]() 有何数量关系?
有何数量关系?
(3)写出所有符合条件的整数点![]() ,使它到10和-10的距离之和为span>20,并求所有这些整数的数的和;
,使它到10和-10的距离之和为span>20,并求所有这些整数的数的和;
(4)找出(3)中满足到10和-10的距离之差大于1而小于5的整数的点![]() ;
;
(5)若点![]() 表示的数为
表示的数为![]() ,当点
,当点![]() 在什么位置时,
在什么位置时,![]() 取得的值最小,并求出这个最小值.
取得的值最小,并求出这个最小值.
【答案】(1)2、4、5、8;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,0,和
,0,和![]() ;(4)
;(4)![]() ,
,![]() ;(5)
;(5)![]() ,最小值5.
,最小值5.
【解析】
(1)根据数轴的知识,结合表格中的数即可得出答案.
(2)由(1)所填写的数字,即可得出结论.
(3)由数轴的知识,可得出只要在-10和10之间的整数均满足题意.
(4)根据(3)的式子即可得到结果;
(5)根据绝对值的几何意义,可得出-1和4之间的任何一点均满足题意.
解:(1)填表如下:
| 6 | -1 | -2 | 4 |
| 4 | -5 | 3 | -4 |
| 2 | 4 | 5 | 8 |
(2)由(1)可得:d=|a-b|或d=|b-a|;
(3)只要在-10和10之间的整数均满足到-10和10的距离之和为20,有:-10、-9、-8、-7、-6、-5、-4、-3、-2、-1、0、1、2、3、4、5、6、7、8、9、10,
所有满足条件的整数之和为:-10+(-9)+(-8)+(-7)+(-6)+(-5)+(-4)+(-3)+(-2)+(-1)+0+1+2+3+4+5+6+7+8+9+10=0;
(4)根据数轴的意义可得,由(3)中的数满足到10和-10的距离之差大于1而小于5的整数的点有数:±2,±1.
(5)因为![]()
所以根据数轴的几何意义可得-1和4之间的任何一点均能使|x+1|+|x-4|取得的值最小.这个最小值是:4-(-1)=5

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】滨海新区某中学为了了解学生每周在校体育锻炼的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了不完整的统计图表,请根据图表信息解答下列问题
时间(小时) | 频数(人数) | 百分比 |
2≤t<3 | 4 | 10% |
3≤t<4 | 10 | 25% |
4≤t<5 | a | 15% |
5≤t<6 | 8 | b% |
6≤t<7 | 12 | 30% |
合计 | 40 | 100% |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
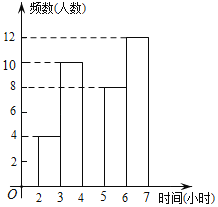
(3)若绘制扇形统计图,时间段6≤x<7所对应扇形的圆心角的度数是多少?
(4)若该校共有1200名学生,估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?