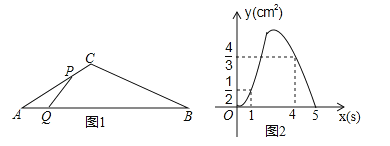题目内容
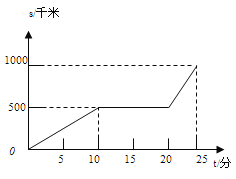
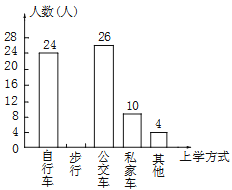
【题目】甲、乙两公司同时销售一款进价为40元/千克的产品.图①中折线ABC表示甲公司销售价y1(元/千克)与销售量x(千克)之间的函数关系,图②中抛物线表示乙公司销售这款产品获得的利润y2(元)与销售量x(千克)之间的函数关系.


(1)分别求出图①中线段AB、图②中抛物线所表示的函数表达式;
(2)当该产品销售量为多少千克时,甲、乙两公司获得的利润的差最大?最大值为多少?
【答案】(1)y2=―0.4(x―75)2+2250;(2)当销售量为50千克时,甲乙两公司获得的利润的差最大,最大是500元.
【解析】分析:(1)由图象可知y与x之间是一次函数关系,可设y=kx+b,把(0,120),(80,72)代入可得;(2)根据:销售利润W=该产品每千克利润×销售量,列出函数关系式,配成二次函数顶点式,结合自变量取值范围可得其最值.
详解:(1)设y1与x之间的函数表达式为y1=kx+b.
根据题意,当x=0时,y1=120;当x=80时,y1=72.
所以![]() ,解得
,解得![]()
所以,y1与x之间的函数表达式为y1=-0.6x+120.
设y2与x之间的函数表达式为y2=a(x―75)2+2250,
当x=0时,y2=0,解得a=―0.4.
所以,y2与x之间的函数表达式为y2=―0.4(x―75)2+2250.
(2)解:设甲、乙两公司的销售总利润的差为w(元).
当0<x≤80时,
w=(y1-40)x―y2= (-0.6x+120―40)x-[(-0.4(x―75)2+2250]
=-0.2x2+20x=-0.2(x-50)2+500.
∵-0.2<0,0<x≤80
∴当x=50时, w有最大值,最大值为500.
当80<x≤84时,
w=(72―40)x―[―0.4(x―75)2+2250]=0.4x2―28x,
∵当80<x≤84时,w随x的增大而增大,
∴当x=84时, 有最大值,最大值为470.4.
综上所述,当销售量为50千克时,甲乙两公司获得的利润的差最大,最大是500元.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案