题目内容
【题目】在一只不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,然后把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
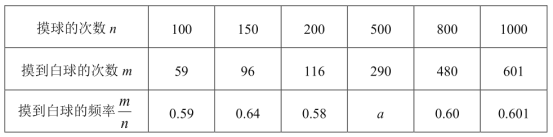
(1)上表中的a= ;
(2)“摸到白球”的概率的估计值是 (精确到0.1)
(3)试估算口袋中黑、白两种颜色的球各有多少个?
【答案】(1) 0.58;(2) 0.6;(3)白球12(个),黑球8 (个)
【解析】
(1)利用频率=频数÷样本容量直接求解即可;
(2)根据统计数据,当n很大时,摸到白球的频率接近0.60;
(3)根据利用频率估计概率,可估计摸到白球的概率为0.60,然后利用概率公式计算白球的个数.
(1)a=![]() =0.58,
=0.58,
故答案为:0.58;
(2)随着实验次数的增加“摸到白球”的频率趋向于0.60,所以其概率的估计值是0.60,
故答案为:0.60;
(3)由(2)摸到白球的概率估计值为0.60,
所以可估计口袋中白种颜色的球的个数=20×0.6=12(个),黑球2012=8(个).
答:黑球8个,白球12个.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目