ЬтФПФкШн
ЁОЬтФПЁПЬНОПгыЗЂЯжЃКШчЭМ1ЫљЪОЕФЭМаЮЃЌЯёЮвУЧГЃМћЕФбЇЯАгУЦЗЉЉдВЙцЃЎЮвУЧВЛЗСАбетбљЭМаЮНазіЁАЙцаЮЭМЁБЃЎ
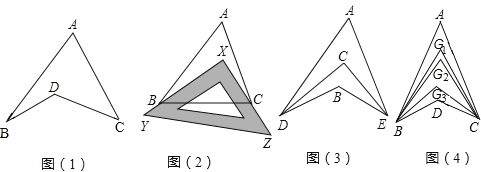
ЃЈ1ЃЉЙлВьЁАЙцаЮЭМЁБЃЌЪдЬНОПЁЯBDCгыЁЯAЁЂЁЯBЁЂЁЯCжЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЧыФужБНгРћгУвдЩЯНсТлЃЌНтОівдЯТШ§ИіЮЪЬтЃК
ЂйШчЭМ2ЃЌАбвЛПщШ§НЧГпXYZЗХжУдкЁїABCЩЯЃЌЪЙШ§НЧГпЕФСНЬѕжБНЧБпXYЁЂXZЧЁКУОЙ§ЕуBЁЂCЃЌЁЯA=40ЁуЃЌдђЁЯABX+ЁЯACX=ЁЁ ЁЁЁуЃЛ
ЂкШчЭМ3ЃЌDCЦНЗжЁЯADBЃЌECЦНЗжЁЯAEBЃЌШєЁЯDAE=40ЁуЃЌЁЯDBE=130ЁуЃЌЧѓЁЯDCEЕФЖШЪ§ЃЛ
ЂлШчЭМ4ЃЌЁЯABDЃЌЁЯACDЕФ10ЕШЗжЯпЯрНЛгкЕуG1ЁЂG2ЁЁЂG9ЃЌШєЁЯBDC=133ЁуЃЌЁЯBG1C=70ЁуЃЌЧѓЁЯAЕФЖШЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЁЯBDC=ЁЯA+ЁЯB+ЁЯCЃЛЃЈ2ЃЉЂй50ЁуЃЛЂк85ЁуЃЛЂл63Ёу.
ЁОНтЮіЁП
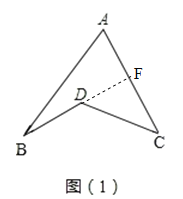
ЃЈ1ЃЉбгГЄBDНЛACгкFЃЌИљОнЭтНЧЕФаджЪЃЌМДПЩХаЖЯГіЁЯBDC=ЁЯBAC+ЁЯB+ЁЯCЃЎ
ЃЈ2ЃЉЂйгЩЃЈ1ЃЉПЩЕУЁЯABX+ЁЯACX+ЁЯA=ЁЯBXCЃЌШЛКѓИљОнЁЯA=40ЁуЃЌЁЯBXC=90ЁуЃЌМДПЩЧѓГіЁЯABX+ЁЯACXЕФжЕЃЎ
ЂкгЩЃЈ1ЃЉПЩЕУЁЯDBE=ЁЯDAE+ЁЯADB+ЁЯAEBЃЌдйИљОнЁЯDAE=40ЁуЃЌЁЯDBE=130ЁуЃЌЧѓГіЁЯADB+ЁЯAEBЕФжЕЃЛШЛКѓИљОнЁЯDCE![]() ЃЈЁЯADB+ЁЯAEBЃЉ+ЁЯDAEЃЌМДПЩЧѓГіЁЯDCEЕФЖШЪ§ЃЎ
ЃЈЁЯADB+ЁЯAEBЃЉ+ЁЯDAEЃЌМДПЩЧѓГіЁЯDCEЕФЖШЪ§ЃЎ
ЂлИљОнЁЯBG1C![]() ЃЈЁЯABD+ЁЯACDЃЉ+ЁЯAЃЌЁЯBG1C=70ЁуЃЌЩшЁЯAЮЊxЁуЃЌПЩЕУЁЯABD+ЁЯACD=133ЁуЉxЁуЃЌНтЗНГЬЃЌЧѓГіxЕФжЕЃЌМДПЩХаЖЯГіЁЯAЕФЖШЪ§ЃЎ
ЃЈЁЯABD+ЁЯACDЃЉ+ЁЯAЃЌЁЯBG1C=70ЁуЃЌЩшЁЯAЮЊxЁуЃЌПЩЕУЁЯABD+ЁЯACD=133ЁуЉxЁуЃЌНтЗНГЬЃЌЧѓГіxЕФжЕЃЌМДПЩХаЖЯГіЁЯAЕФЖШЪ§ЃЎ
ЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌбгГЄBDНЛACгкFЃЌИљОнЭтНЧЕФаджЪЃЌПЩЕУЃКЁЯDFC=ЁЯA+ЁЯBЃЎ
ЁпЁЯBDC=ЁЯDFC+ЁЯCЃЌЁрЁЯBDC=ЁЯA+ЁЯB+ЁЯCЃЛ
ЃЈ2ЃЉЂйгЩЃЈ1ЃЉЃЌПЩЕУЃКЁЯABX+ЁЯACX+ЁЯA=ЁЯBXCЃЎ
ЁпЁЯA=40ЁуЃЌЁЯBXC=90ЁуЃЌЁрЁЯABX+ЁЯACX=90ЁуЉ40Ёу=50ЁуЃЎ
ЙЪД№АИЮЊЃК50ЃЎ
ЂкгЩЃЈ1ЃЉЃЌПЩЕУЃКЁЯDBE=ЁЯDAE+ЁЯADB+ЁЯAEBЃЌЁрЁЯADB+ЁЯAEB=ЁЯDBEЉЁЯDAE=130ЁуЉ40Ёу=90ЁуЃЌЁр![]() ЃЈЁЯADB+ЁЯAEBЃЉ=90ЁуЁТ2=45ЁуЃЌЁрЁЯDCE
ЃЈЁЯADB+ЁЯAEBЃЉ=90ЁуЁТ2=45ЁуЃЌЁрЁЯDCE![]() ЃЈЁЯADB+ЁЯAEBЃЉ+ЁЯDAE=45Ёу+40Ёу=85ЁуЃЛ
ЃЈЁЯADB+ЁЯAEBЃЉ+ЁЯDAE=45Ёу+40Ёу=85ЁуЃЛ
ЂлЁЯBG1C![]() ЃЈЁЯABD+ЁЯACDЃЉ+ЁЯAЃЎ
ЃЈЁЯABD+ЁЯACDЃЉ+ЁЯAЃЎ
ЁпЁЯBG1C=70ЁуЃЌЁрЩшЁЯAЮЊxЁуЃЎ
ЁпЁЯABD+ЁЯACD=133ЁуЉxЁу
Ёр![]() ЃЈ133ЉxЃЉ+x=70ЃЌЁр13.3
ЃЈ133ЉxЃЉ+x=70ЃЌЁр13.3![]() x+x=70ЃЌНтЕУЃКx=63ЃЌМДЁЯAЕФЖШЪ§ЮЊ63ЁуЃЎ
x+x=70ЃЌНтЕУЃКx=63ЃЌМДЁЯAЕФЖШЪ§ЮЊ63ЁуЃЎ

 НзЬнМЦЫуЯЕСаД№АИ
НзЬнМЦЫуЯЕСаД№АИ