题目内容
【题目】如图1,长方形![]() 放置在平面直角坐标系中,已知点
放置在平面直角坐标系中,已知点![]() ,点
,点![]() ,动点
,动点![]() 从
从![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位的速度运动,同时,动点
个单位的速度运动,同时,动点![]() 从
从![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位的速度运动.当其中一点到达
个单位的速度运动.当其中一点到达![]() 点时,两动点同时停止运动设运动时间为
点时,两动点同时停止运动设运动时间为![]() .
.

(1)当![]() ______时,点
______时,点![]() 追上点
追上点![]() ,此时点
,此时点![]() 的坐标为_______.
的坐标为_______.
(2)当![]() 时,分别取
时,分别取![]() 、
、![]() 的中点
的中点![]() 、
、![]() ,如果四边形
,如果四边形![]() 的面积等于
的面积等于![]() ,请求出时间
,请求出时间![]() 的取值;
的取值;
(3)如图2,连接![]() ,已知
,已知![]() ,在(2)问的条件下,过点
,在(2)问的条件下,过点![]() 作
作![]() 于点
于点![]() ,问在长方形
,问在长方形![]() 的四条边上是否存在点
的四条边上是否存在点![]() ,使得线段
,使得线段![]() ,若存在,请直接写出点
,若存在,请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)4s,(6,6);(2)![]() 或
或![]() ;(3)存在,点N的坐标为
;(3)存在,点N的坐标为 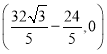 或
或 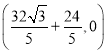 或
或 ![]() 或
或 ![]()
【解析】
(1)根据速度差×追击时间=追击距离,构建方程即可解决问题.
(2)分两种情形:如图1中,当0<t<2时,S四边形OEQF=S四边形OAQF-S△AEQ=18,如图2中,当2<t≤3时,S四边形OEQF=SOPQF-S△EPQ=18,分别构建方程求解即可.
(3)根据(2)中两种情形,画出图形利用相似三角形的性质求出PM,即可解决问题.
解:(1)∵A(8,0),C(0,6),四边形OABC是矩形,
∴OA=BC=8,AB=OC=6,
设t秒后追上.
由题意:4t-2t=8,
∴t=4.
∴P(6,6).
故答案为4s,(6,6).
(2)如图1中,当0<t<2时,S四边形OEQF=S四边形OAQF-S△AEQ=18,
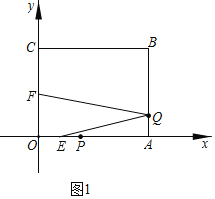
![]()
解得 ![]() 或
或![]() (舍)
(舍)
如图2中,当![]() 时
时![]()
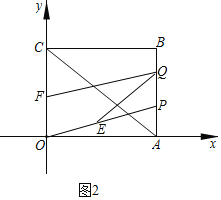
∴![]() (3+8-2t)8-
(3+8-2t)8-![]() (8-2t)4=18,
(8-2t)4=18,
∴t=![]() .
.
(3)如图3中连接CP,当t=![]() 时,P(4
时,P(4![]() ,0),
,0),

![]()
![]()
![]()
![]()
![]()
点 ![]() 在OA边上
在OA边上 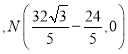 或
或 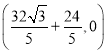
当 ![]() 时
时 ![]() 如图3-2中,同法可得
如图3-2中,同法可得 ![]()

![]()
![]() 点
点![]() 在边
在边![]() 上,
上,![]() 或
或 ![]()
综上所述,满足条件的点N的坐标为 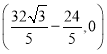 或
或 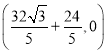 或
或 ![]() 或
或 ![]()

【题目】今年10月份某商场用19600元同时购进A、B两种新型节能日光灯共440盏,A型日光灯每盏进价为40元,售价为60元,B型日光灯每盏进价为50元,售价为80元.
(1)求10月份两种新型节能日光灯各购进多少盏?
(2)将10月份购买的日光灯从生产基地运往商场的过程中,A型日光灯出现![]() 的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润
的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润![]() 型日光灯在原售价基础上提高
型日光灯在原售价基础上提高![]() ,问A型日光灯调整后的售价为多少元?
,问A型日光灯调整后的售价为多少元?
(3)进入11月份,B型日光灯的需求量增大,于是商场在筹备“双十一”促销活动时,决定去甲、乙两个生产基地只购进一批B型日光灯,甲、乙生产基地给出了不同的优惠措施:
甲生产基地:B型日光灯出厂价为每盏50元,折扣如表一所示
乙生产基地:B型日光灯出厂价为每盏47元,同时当出厂总金额达一定数量后还可按表二返现金.
表一
甲生产基地 | |
一次性购买的数量 | 折扣数 |
不超过150盏的部分 |
|
超过150盏的部分 | 9折 |
表二
乙生产基地 | |
出厂总金额 | 返现金 |
不超过5640元 | 0元 |
超过5640元,但不超过9353元 | 返现300元 |
超过9353元 | 先返现出厂总金额的 |
已知该商场在甲生产基地购买B型日光灯共支付7350元,在乙生产基地购买B型日光灯共支付9006元,若将在两个生产基地购买的B型日光灯的总量改由在乙生产基地一次性购买,则支付总金额比在甲、乙两生产基地分别购买的支付金额之和可节约多少元?