题目内容
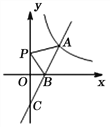
【题目】如图,一次函数y=2x+b的图象与反比例函数![]() (x>0)的图象交于点A(m,2),与坐标轴分别交于B和C(0,-2)两点.
(x>0)的图象交于点A(m,2),与坐标轴分别交于B和C(0,-2)两点.
(1)求反比例函数的表达式;
(2)若P是y轴上一动点,当PA+PB的值最小时,求点P的坐标.
【答案】(1)y=![]() ;(2)点P的坐标为(0,
;(2)点P的坐标为(0,![]() ).
).
【解析】分析:(1)先把C(0,-2)代入y=2x+b中求出b的值,得出解析式.点A(m,2)也在一次函数上所以可以求出m的值,然后把点A代入反比例函数![]() (x>0),求出k值即可.(2)作B点关于y轴对称的点B′,连接AB′,交于y轴于点P,由轴对称的性质可知:PA+PB=PA+PB,= AB,,两点之间直线最短,即可求解.
(x>0),求出k值即可.(2)作B点关于y轴对称的点B′,连接AB′,交于y轴于点P,由轴对称的性质可知:PA+PB=PA+PB,= AB,,两点之间直线最短,即可求解.
(1)∵点C (0,-2)在直线![]() 上,
上,
∴b=-2,直线为![]() ,
,
∵点A(m,2)在直线为![]() 上,∴
上,∴![]() ,m=2,
,m=2,
∵点A(2,2)在反比例函数y=![]() 的图象上,
的图象上,
∴2=![]() ,k=4,∴反比例函数的表达式y=
,k=4,∴反比例函数的表达式y=![]() .
.
(2)由![]() ,令y=0,得:x=1,∴B(1,0),
,令y=0,得:x=1,∴B(1,0),
如图,设点B(1,0)关于y轴对称的点为B′,
则B,(-1,0),
连接AB,交y轴于点P,
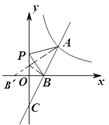
此时,PA+PB=PA+PB,= AB,,
∵两点之间线段最短,
∴所求的点P就是直线AB,与y轴的交点,
∵由A(2,2)和B,(-1,0)确定的直线为y=![]() ,
,
∴所求点P的坐标为(0,![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
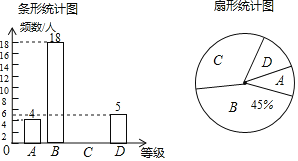
小学生10分钟应用题系列答案【题目】今年5月19日为第29个“全国助残日”我市某中学组织了献爱心捐款活动,该校数学课外活动小组对本次捐款活动做了一次抽样调查,并绘制了如下不完整的频数分布表和频数分布直方图(每组含前一个边界,不含后一个边界).
捐款额(元) | 频数 | 百分比 |
| 3 | 7.5% |
| 7 | 17.5% |
| a | b |
| 10 | 25% |
| 6 | 15% |
总计 | 100% |
(1)填空:![]() ________,
________,![]() ________.
________.
(2)补全频数分布直方图.
(3)该校有2000名学生估计这次活动中爱心捐款额在![]() 的学生人数.
的学生人数.
【题目】我们在生活中经常使用的数是十进制数,如![]() ,表示十进制的数要用到10个数码(也叫数字):0,1,2,3,4,5,6,7,8,9.计算机中常用的十六进制是逢16进1的计数制,采用数字
,表示十进制的数要用到10个数码(也叫数字):0,1,2,3,4,5,6,7,8,9.计算机中常用的十六进制是逢16进1的计数制,采用数字![]() 和字母
和字母![]() 共16个计数符号,这些符号与十进制的对应关系如下表
共16个计数符号,这些符号与十进制的对应关系如下表
十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如:十六进制数![]() ,即十六进制数71B相当于十进制数1819.那么十六进制数2E8相当于十进制数( )
,即十六进制数71B相当于十进制数1819.那么十六进制数2E8相当于十进制数( )
A.744B.736C.536D.512