题目内容
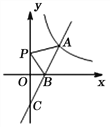
【题目】如图①,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,将一直角三角板如图摆放(
,将一直角三角板如图摆放(![]() ).
).
(1)若![]() ,求
,求![]() 的大小.
的大小.
(2)将图①中的三角板绕点![]() 旋转一定的角度得图②,使边
旋转一定的角度得图②,使边![]() 恰好平分
恰好平分![]() ,问:
,问:![]() 是否平分
是否平分![]() ?请说明理由.
?请说明理由.
(3)将图①中的三角板绕点![]() 旋转一定的角度得图③,使边
旋转一定的角度得图③,使边![]() 在
在![]() 的内部,如果
的内部,如果![]() ,则
,则![]() 与
与![]() 之间存在怎样的数量关系?请说明理由.
之间存在怎样的数量关系?请说明理由.

【答案】(1)125°;(2)ON平分∠AOC,理由详见解析;(3)∠BOM=∠NOC+40°,理由详见解析
【解析】
(1)根据∠MOC=∠MON+∠BOC计算即可;
(2)由角平分线定义得到角相等的等量关系,再根据等角的余角相等即可得出结论;
(3)根据题干已知条件将一个角的度数转换为两个角的度数之和,列出等式即可得出结论.
解: (1) ∵∠MON=90° , ∠BOC=35°,
∴∠MOC=∠MON+∠BOC= 90°+35°=125°.
(2)ON平分∠AOC.
理由如下:
∵∠MON=90°,
∴∠BOM+∠AON=90°,∠MOC+∠NOC=90°.
又∵OM平分∠BOC,∴∠BOM=∠MOC.
∴∠AON=∠NOC.
∴ON平分∠AOC.
(3)∠BOM=∠NOC+40°.
理由如下:
∵∠CON+∠NOB=50°,∴∠NOB=50°-∠NOC.
∵∠BOM+∠NOB=90°,
∴∠BOM=90°-∠NOB=90°-(50°-∠NOC)=∠NOC+40°.

 名校课堂系列答案
名校课堂系列答案【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:
型号 | 甲 | 乙 |
每台每小时分拣快递件数(件) | 1000 | 800 |
每台价格(万元) | 5 | 3 |
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?