题目内容
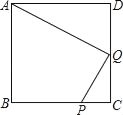
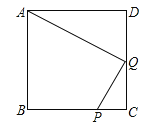
【题目】如图,P是正方形ABCD边BC上的一点,且BP=3PC,Q是CD中点.
(1)求证:△ADQ∽△QCP.
(2)试问:AQ与PQ有什么关系(位置与数量)?
【答案】(1)见解析;(2)AQ=2PQ,且AQ⊥PQ.理由见解析
【解析】分析:(1)在所要求证的两个三角形中,已知的等量条件为:∠D=∠C=90°,若证明两三角形相似,可证两个三角形的对应直角边成比例;
(2)AQ=2PQ,且AQ⊥PQ.根据相似三角形的对应边成比例即可求得AQ与PQ的数量关系;根据相似三角形的对应角相等即可证得AQ与PQ的位置关系.
详解:(1)∵四边形ABCD是正方形,∴AD=CD,∠C=∠D=90°;
又∵Q是CD中点,∴CQ=DQ=![]() AD;
AD;
∵BP=3PC,∴CP=![]() AD,∴
AD,∴![]() =
=![]() =
=![]() .
.
又∵∠C=∠D=90°,∴△ADQ∽△QCP;
(2)AQ=2PQ,且AQ⊥PQ.理由如下:
由(1)知,△ADQ∽△QCP,![]() =
=![]() =
=![]() ,则
,则![]() =
=![]() =
=![]() =
=![]() ,AQ=2PQ;
,AQ=2PQ;
∵△ADQ∽△QCP,∴∠AQD=∠QPC,∠DAQ=∠PQC,
∴∠PQC+∠DQA=DAQ+AQD=90°,∴AQ⊥QP.

练习册系列答案
相关题目
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:
型号 | 甲 | 乙 |
每台每小时分拣快递件数(件) | 1000 | 800 |
每台价格(万元) | 5 | 3 |
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?