题目内容
【题目】如图,在![]() 中,
中,![]() 度.以
度.以![]() 的三边为边分别向外作等边三角形
的三边为边分别向外作等边三角形![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() 的面积分别是8和3,则
的面积分别是8和3,则![]() 的面积是( )
的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
【答案】D
【解析】
先设AC=b,BC=a,AB=c,根据勾股定理有c2+b2=a2,再根据等式性质可得![]() c2+
c2+![]() b2=
b2=![]() a2,再根据等边三角形的性质以及特殊三角函数值,易求得S3=
a2,再根据等边三角形的性质以及特殊三角函数值,易求得S3=![]() ×sin60°aa=
×sin60°aa=![]() a2,同理可求S2=
a2,同理可求S2=![]() b2,S1=
b2,S1=![]() c2,从而可得S1+S2=S3,易求S1.
c2,从而可得S1+S2=S3,易求S1.
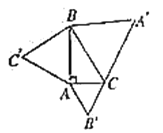
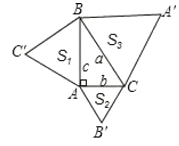
解:如图,设等边三角形△A'BC,△AB'C,△ABC'的面积分别是S3,S2,S1,
设AC=b,BC=a,AB=c,
∵△ABC是直角三角形,且∠BAC=90度,
∴c2+b2=a2,
∴![]() c2+
c2+![]() b2=
b2=![]() a2,
a2,
又∵S3=![]() ×sin60°aa=
×sin60°aa=![]() a2,同理可求S2=
a2,同理可求S2=![]() b2,S1=
b2,S1=![]() c2,
c2,
∴S1+S2=S3,
∵S3=8,S2=3,
∴S1=S3S2=83=5,
故选:D.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目