题目内容
【题目】为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查,一测量船在A岛测得B岛在北偏西30°,C岛在北偏东15°,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离( ![]() ≈2.45,结果保留到整数)
≈2.45,结果保留到整数) 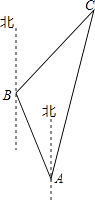
【答案】解:由题意知:∠BAC=45°,∠FBA=30°,∠EBC=45°,AB=100海里;
过B点作BD⊥AC于点D,
∵∠BAC=45°,
∴△BAD为等腰直角三角形;
∴BD=AD=50 ![]() ,∠ABD=45°;
,∠ABD=45°;
∴∠CBD=180°﹣30°﹣45°﹣45°=60°,
∴∠C=30°;
∴在Rt△BCD中BC=100 ![]() ≈141海里,CD=50
≈141海里,CD=50 ![]() ,
,
∴AC=AD+CD=50 ![]() +50
+50 ![]() ≈193海里.
≈193海里.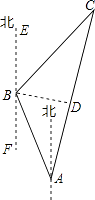
【解析】本题考查的是解直角三角形的应用﹣方向角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.过点B作BD⊥AC于点D,由等腰直角三角形的性质求出AD的长,再由直角三角形的性质即可得出结论.
【考点精析】根据题目的已知条件,利用关于方向角问题的相关知识可以得到问题的答案,需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目