题目内容
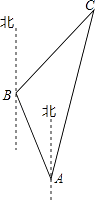
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为 
【答案】4或7或9
【解析】解: 在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,
∴AB=2BC=8cm,
∵D为BC中点,
∴BD=2cm,
∵0≤t<12,
∴E点的运动路线为从A到B,再从B到AB的中点,
按运动时间分为0≤t≤8和8<t<12两种情况,
①当0≤t≤8时,AE=tcm,BE=BC﹣AE=(8﹣t)cm,
当∠EDB=90°时,则有AC∥ED,
∵D为BC中点,
∴E为AB中点,
此时AE=4cm,可得t=4;
当∠DEB=90°时,
∵∠DEB=∠C,∠B=∠B,
∴△BED∽△BCA,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得t=7;
,解得t=7;
②当8<t<12时,则此时E点又经过t=7秒时的位置,此时t=8+1=9;
综上可知t的值为4或7或9,
所以答案是:4或7或9.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.

【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是 ![]() ;
;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
A.①②③
B.②③④
C.②③
D.①④