题目内容
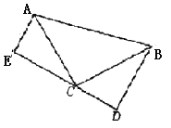
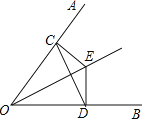
【题目】如图,在△ABC中,AB=AC,点D为BC上一点,以AD为腰作等腰△ADE,AD=AE,∠BAC=∠DAE,连接CE.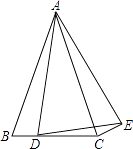
(1)求证:BD=CE;
(2)已知BC=8,∠BAC=∠DAE=30°,若△DCE的面积为1,求线段BD的长.
【答案】
(1)
证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠EAC,
在△ABD和△ACE中,
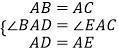 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)
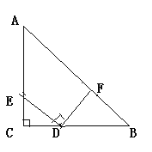
解: 过D作DF⊥EC交EC的延长线于F,
∵△ABD≌△ACE,
∴∠ACE=∠B,
∵∠BAC=30°,
∴∠B+∠ACB=150°,
∴∠BCE=∠ACB+∠ACE=150°,
∴∠DCF=30°,
∴DF= ![]() CD=
CD= ![]() (BC﹣BD)=
(BC﹣BD)= ![]() (8﹣BD),
(8﹣BD),
∵CE=BD,
∴DF=4﹣ ![]() CE,
CE,
∵△DCE的面积为1,
∴ ![]() DFCE=
DFCE= ![]() CFBD=
CFBD= ![]() (8﹣BD)BD=1,
(8﹣BD)BD=1,
解得:BD=4﹣ ![]() ,BD=4+
,BD=4+ ![]() (不合题意,舍去).
(不合题意,舍去).
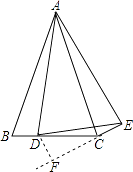
【解析】(1)易证∠BAD=∠EAC,即可证明△ABD≌△ACE,即可得到结论;(2)过D作DF⊥EC交EC的延长线于F,由△ABD≌△ACE,得到∠ACE=∠B,根据∠BAC=30°,于是得到∠B+∠ACB=150°,等量代换得到∠BCE=∠ACB+∠ACE=150°,由邻补角的性质得到∠DCF=30°,根据直角三角形的性质得到DF= ![]() CD=
CD= ![]() (BC﹣BD)=
(BC﹣BD)= ![]() (8﹣BD),根据△DCE的面积为1,列方程即可得到结论.
(8﹣BD),根据△DCE的面积为1,列方程即可得到结论.
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等.

练习册系列答案
相关题目