题目内容
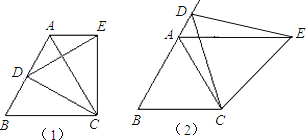
【题目】(如图1,等边△ABC中,D是AB边上的点,以CD为一边,向上作等边△EDC,连接AE.
(1)求证:△DBC≌△EAC;
(2)求证:AE∥BC;
(3)如图2, 若D在边BA的延长线上,且AB=6,AD=2,试求△ABC与△EAC面积的比值.
【答案】(1)详见解析,(2)详见解析,(3)![]() .
.
【解析】
(1)已知的条件有AC=BC,CE=CD,我们发现∠BCD和∠ACE都是60°减去一个∠ACD,因此两三角形全等的条件就都凑齐了(SAS);
(2)要证AE∥BC,关键是证∠EAC=∠ACB,由于∠ACB=∠ACB,那么关键是证∠EAC=∠ACB,根据(1)的全等三角形,我们不难得出这两个角相等,也就得出了证平行的条件.
(3)同(1)(2)的思路完全相同,也是通过先证明△BCD和△ACE全等,即可得到△ABC与△EAC面积的比值.
(1)证明:∵∠ACB=60°,∠DCE=60°,
∴∠BCD=60°∠ACD,∠ACE=60°∠ACD,
∴∠BCD=∠ACE,
在△DBC和△EAC中,
∵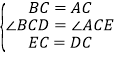 ,
,
∴△DBC≌△EAC(SAS),
(2)∵△DBC≌△EAC,
∴∠EAC=∠B=60°,
又∠ACB=60°,
∴∠EAC=∠ACB,
∴AE∥BC;
(3)结论:AE∥BC,
理由:∵△ABC、△EDC为等边三角形,
∴BC=AC,DC=CE,∠BCA=∠DCE=60°,
∠BCA+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,
在△DBC和△EAC中,
∵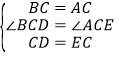 ,
,
∴△DBC≌△EAC(SAS),
∴∠EAC=∠B=60°,AE=BD
又∠ACB=60°,
∴∠EAC=∠ACB,
∴AE∥BC;
设AE,BC两平行线间的距离为h
∵AB=6,AD=2,
∴S△ABC=![]() BCh=
BCh=![]() ×6h=3h,
×6h=3h,
S△ACE=![]() AEh=
AEh=![]() ×8h=4h
×8h=4h
∴S△ABC∶S△AEC=![]()
则△ABC与△EAC面积的比值为![]() .
.

 新思维寒假作业系列答案
新思维寒假作业系列答案