题目内容
【题目】为了估计鱼塘中成品鱼(个体质量在0.5kg及以上,下同)的总质量,先从鱼塘中捕捞50条成品鱼,称得它们的质量如表:
质量/kg | 0.5 | 0.6 | 0.7 | 1.0 | 1.2 | 1.6 | 1.9 |
数量/条 | 1 | 8 | 15 | 18 | 5 | 1 | 2 |
然后做上记号再放回水库中,过几天又捕捞了100条成品鱼,发现其中2条带有记号.
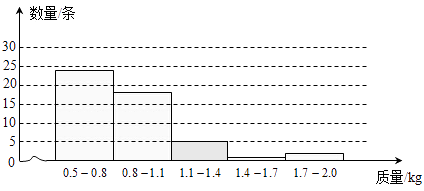
(1)请根据表中数据补全如图的直方图(各组中数据包括左端点不包括右端点). 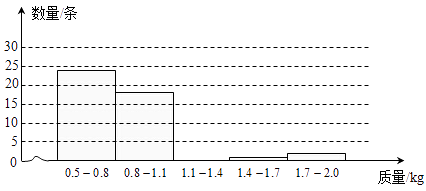
(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)根据图中数据分组,估计鱼塘里质量中等的成品鱼,其质量落在哪一组内?
(4)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1kg).
【答案】
(1)解:由函数图象可以得出1.1﹣1.4的有5条,补全图形,得:
(2)解:由题意,得
0.5﹣0.8的频率为:24÷50=0.48,
0.8﹣1.1的频率为:18÷50=0.36,
1.1﹣1.4的频率为:5÷50=0.1,
1.4﹣1.7的频率为:1÷50=0.02,
1.7﹣2.0的频率为:2÷50=0.04.
∵0.48>0.36>0.1>0.04>0.02.
∴估计从鱼塘中随机捕一条成品鱼,其质量落在0.5﹣0.8的可能性最大
(3)解:这组数据的个数为50,就可以得出第25个和第26个数分别是1.0,1.0,
∴(1.0+1.0)÷2=1.0,
鱼塘里质量中等的成品鱼,其质量落在0.8﹣1.1内
(4)解:设鱼塘中成品鱼的条数为x,由题意,得:
50:x=2:100,
解得:x=2500.
2500× ![]() =2260kg
=2260kg
【解析】(1)由函数图象可以得出1.1﹣1.4的有5条,就可以补全直方图;(2)分别求出各组的频率,就可以得出结论;(3)由这组数据的个数为50,就可以得出第25个和第26个数的平均数就可以得出结论;(4)设鱼塘中成品鱼的条数为x,根据作记号的鱼50:x=2:100建立方程求出其解即可.
【考点精析】本题主要考查了频数分布直方图的相关知识点,需要掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图)才能正确解答此题.