题目内容
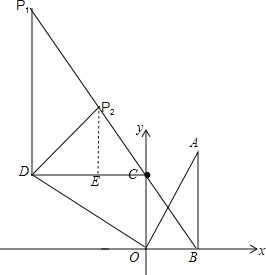
【题目】如图,Rt△ABO在平面直角坐标系中,O为原点,OB在x轴上,∠AOB=60°,点A坐标为(3,3![]() ),点C的坐标为(0,3),点D在第二象限,且△ABO≌△DCO.
),点C的坐标为(0,3),点D在第二象限,且△ABO≌△DCO.

(1)请直接写出点D的坐标_____;
(2)点P在直线BC上,且△PCD是等腰直角三角形,请画出图形并求点P的坐标.
【答案】(1)D(﹣3![]() ,3);(2)画图形见解析,点P在直线BC上,使△PCD是等腰直角三角形的点P的坐标为(
,3);(2)画图形见解析,点P在直线BC上,使△PCD是等腰直角三角形的点P的坐标为(![]() ,3+
,3+![]() ),(
),(![]() ,
,![]() ).
).
【解析】
(1)由△ABO≌△DCO,利用全等三角形的性质可得CD=BA,由点A坐标为(3,3![]() ),点C的坐标为(0,3),可得D点的坐标;
),点C的坐标为(0,3),可得D点的坐标;
(2)首先利用全等三角形的性质可得OC=OB=3,∠BOC=90°,易得∠OBC=45°,分类讨论当CD为直角边时,过点D作P1D⊥CD,交BC于点P1,由DC∥OB,可得
△P1DC为等腰直角三角形,易得![]() ,可得P1点的坐标;当CD为斜边时,过D点作DP2⊥BC交BC于点P2,易得△CDP2是等腰直角三角形,作P2E⊥CD,可得CE=DE=
,可得P1点的坐标;当CD为斜边时,过D点作DP2⊥BC交BC于点P2,易得△CDP2是等腰直角三角形,作P2E⊥CD,可得CE=DE=![]() ,易得P2点的坐标.
,易得P2点的坐标.
(1)点D在第二象限,正确画出△COD如图所示,
∵△ABO≌△DCO,
∴CD=BA,
∵点A坐标为(3,3![]() ),点C的坐标为(0,3),
),点C的坐标为(0,3),
∴D(﹣3![]() ,3),
,3),
故答案为:(﹣3![]() ,3);
,3);
(2)∵OC=OB=3,∠BOC=90°,
∴∠OBC=45°,
①当CD为直角边时,如图,过点D作P1D⊥CD,交BC于点P1,
∵DC∥OB,
∴∠DCP1=∠OBC=45°,
∴△P1DC为等腰直角三角形,
∴![]() ,
,
∴P1(﹣3![]() ,3
,3![]() );
);
②当CD为斜边时,过D点作DP2⊥BC交BC于点P2,
易得△CDP2是等腰直角三角形,作P2E⊥CD,
∵CP2=DP2,
∴CE=DE=![]() ,
,
∴P2(![]() ,
,![]() )..
)..
综上所述,点P在直线BC上,使△PCD是等腰直角三角形的点P的坐标为(![]() ,3
,3![]() ),(
),(![]() ,
,![]() )..
)..

【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目 | 第一年的工资(万元) | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?