题目内容
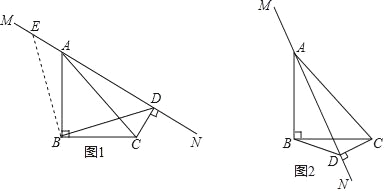
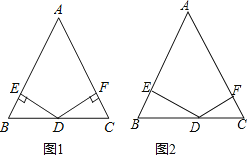
【题目】(1)如图1,等腰三角形ABC中,AB=AC,点D是BC的中点,DE⊥AB与点E、DF⊥AC与点F.求证:DE= DF;
(2)如图2,等腰三角形ABC中,AB=AC=13,BC=10,点D是BC边上的动点,DE⊥AB与点E、DF⊥AC与点F.请问DE+DF的值是否随点D位置的变化而变化?若不变,请直接写出DE+DF的值;若变化,请说明理由.
【答案】(1)见解析;(2)不变;![]() .
.
【解析】
(1)连接![]() ,
,![]() 是
是![]() 的中点,那么
的中点,那么![]() 就是等腰三角形
就是等腰三角形![]() 底边上的中线,根据等腰三角形三线合一的特性,可知道
底边上的中线,根据等腰三角形三线合一的特性,可知道![]() 也是
也是![]() 的角平分线,根据角平分线的点到角两边的距离相等,那么
的角平分线,根据角平分线的点到角两边的距离相等,那么![]() ;
;
(2)连接![]() ,根据三角形的面积公式即可得到
,根据三角形的面积公式即可得到![]() ,进而求得
,进而求得![]() 的值.
的值.
(1)证明:如图1,连接![]() .
.

![]() ,点
,点![]() 是
是![]() 边上的中点,
边上的中点,
![]() 平分
平分![]() ,
,
![]() 、
、![]() 分别垂直
分别垂直![]() 、
、![]() 于点
于点![]() 和
和![]() .
.
![]() .
.
(2)解:不变.
如图2所示:连接![]() ,
,

![]() ,
,![]() ,
,
![]() 底边
底边![]() 上的高
上的高![]() ,
,
![]() 的面积
的面积![]() ,
,
![]()
![]() ,
,
![]() ,
,
故答案为:![]() .
.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目