题目内容
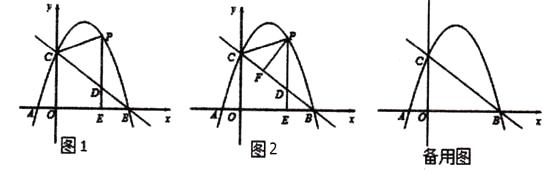
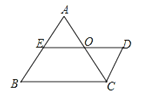
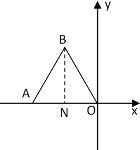
【题目】如图1，等边△OAB的顶点A在x轴的负半轴上，点B（a，b）在第二象限内，且a，b满足
.点P是y轴上的一个动点，以PA为边作等边△PAC，直线BC交x轴于点M，交y轴于点D.
(1)求点A的坐标；
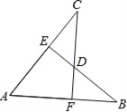
(2)如图2，当点P在y轴正半轴上时，求点M的坐标；
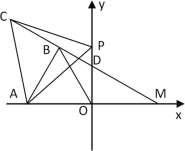
(3)如图3，当点P在y轴负半轴上时，求出OP，CD，AD满足的数量关系，并证明你的结论.
【答案】(1)A（－4，0）；(2)M（4，0）；(3)OP= CD+
AD，证明见解析.
【解析】
（1）如图1中，作BN⊥AO于N．由非负数的性质求出点B坐标即可解决问题；
（2）只要证明△ABC≌△AOP，得出∠ABC=∠AOP=90°，在Rt△ABM中，解直角三角形即可解决问题；
(3)如图3中，取AD的中点R，连接BR、OR．首先证明A、B、D、O四点共圆，推出∠BAD=∠BOD=90°-60°=30°，可得BD=AD，再证明△OAP≌△BAC，可得OP=BC=CD+BD=CD+AD.
（1）如图1中，作BN⊥AO于N．
∵
，
∴a=-2，b=2
，
∴B（-2，2），
∵BA=BO，BN⊥OA，
∴NA=NO=2，
∴OA=4，
∴A（-4，0）．
(2) 如图2中，
∵△ABO，△APC都是等边三角形，
∴∠OAB=∠PAC，OA=OB，AP=AC，
∴∠OAP=∠BAC，
∴△OAP≌△BAC，
∴∠AOP=∠CBA=90°，
在Rt△ABM中，∵∠ABM=90°，AB=OA=4，∠BAM=60°，
∴AM=2AB=8，
∴OM=AM-OA=4，
∴M（4，0）．
(3) 结论：OP=CD+AD．
理由：如图3中，取AD的中点R，连接BR、OR．
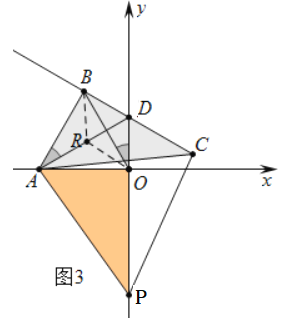
∵∠ABD=∠AOD=90°，AR=DR，
∴BR=AR=RD=OR，
∴A、B、E、O四点共圆，
∴∠BAD=∠BOD=90°-60°=30°，
∴BD=AD，
∵△ABO，△APC都是等边三角形，
∴∠OAB=∠PAC，OA=OB，AP=AC，
∴∠OAP=∠BAC，
∴△OAP≌△BAC，
∴OP=BC=CD+BD=CD+AD．
即OP=CD+AD．
