Question

【题目】如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE= ．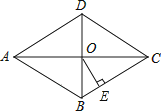

Answer 1

【答案】
【解析】解：∵四边形ABCD为菱形，∴AC⊥BD，OB=OD= BD=3，OA=OC= AC=4，
在Rt△OBC中，∵OB=3，OC=4，
∴BC= =5，
∵OE⊥BC，
∴ OEBC= OBOC，∴OE= = ．故答案为 ．
先根据菱形的性质得AC⊥BD，OB=OD= BD=3，OA=OC= AC=4，再在Rt△OBC中利用勾股定理计算出BC=5，然后利用面积法计算OE的长．本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．也考查了勾股定理和三角形面积公式．