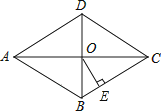
题目内容
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣ ![]() x+1与y轴交于点D.
x+1与y轴交于点D. 
(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=ax2+bx﹣3,
∴c=﹣3,
∴C(0,﹣3),
∴OC=3,
∵BO=OC=3AO,
∴BO=3,AO=1,
∴B(3,0),A(﹣1,0),
∵该抛物线与x轴交于A、B两点,
∴ ![]() ,
,
∴ ![]() ,
,
∴抛物线解析式为y=x2﹣2x﹣3
(2)
证明:由(1)知,抛物线解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴E(1,﹣4),
∵B(3,0),A(﹣1,0),C(0,﹣3),
∴BC=3 ![]() ,BE=2
,BE=2 ![]() ,CE=
,CE= ![]() ,
,
∵直线y=﹣ ![]() x+1与y轴交于点D,
x+1与y轴交于点D,
∴D(0,1),
∵B(3,0),
∴OD=1,OB=3,BD= ![]() ,
,
∴ ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴△BCE∽△BDO
(3)
解:存在,
理由:设P(1,m),
∵B(3,0),C(0,﹣3),
∴BC=3 ![]() ,PB=
,PB= ![]() ,PC=
,PC= ![]() ,
,
∵△PBC是等腰三角形,
①当PB=PC时,
∴ ![]() =
= ![]() ,
,
∴m=﹣1,
∴P(1,﹣1),
②当PB=BC时,
∴3 ![]() =
= ![]() ,
,
∴m=± ![]() ,
,
∴P(1, ![]() )或P(1,﹣
)或P(1,﹣ ![]() ),
),
③当PC=BC时,
∴3 ![]() =
= ![]() ,
,
∴m=﹣3± ![]() ,
,
∴P(1,﹣3+ ![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣ ![]() ),
),
∴符合条件的P点坐标为P(1,﹣1)或P(1, ![]() )或P(1,﹣
)或P(1,﹣ ![]() )或P(1,﹣3+
)或P(1,﹣3+ ![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣ ![]() )
)
【解析】(1)先求出点C的坐标,在由BO=OC=3AO,确定出点B,A的坐标,最后用待定系数法求出抛物线解析式;(2)先求出点A,B,C,D,E的坐标,从而求出BC=3 ![]() ,BE=2
,BE=2 ![]() ,CE=
,CE= ![]() ,OD=1,OB=3,BD=
,OD=1,OB=3,BD= ![]() ,求出比值,得到
,求出比值,得到 ![]() 得出结论;(3)设出点P的坐标,表示出PB,PC,求出BC,分三种情况计算即可.此题是二次函数综合题,主要考查了点的坐标的确定方法,两点间的距离公式,待定系数法,等腰三角形的性质,相似三角形的判定,解本题的关键是判断△BCE∽△BDO.难点是分类.
得出结论;(3)设出点P的坐标,表示出PB,PC,求出BC,分三种情况计算即可.此题是二次函数综合题,主要考查了点的坐标的确定方法,两点间的距离公式,待定系数法,等腰三角形的性质,相似三角形的判定,解本题的关键是判断△BCE∽△BDO.难点是分类.

【题目】某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
选项 | 方式 | 百分比 |
A | 唱歌 | 35% |
B | 舞蹈 | a |
C | 朗诵 | 25% |
D | 器乐 | 30% |
请结合统计图表,回答下列问题:
(1)本次调查的学生共△人,a=△ , 并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式恰好是“唱歌”和“舞蹈”的概率.