题目内容
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式x2﹣4>0
解:∵x2﹣4=(x+2)(x﹣2)
∴x2﹣4>0可化为
(x+2)(x﹣2)>0
由有理数的乘法法则“两数相乘,同号得正”,得
①![]() ②
②![]()
解不等式组①,得x>2,
解不等式组②,得x<﹣2,
∴(x+2)(x﹣2)>0的解集为x>2或x<﹣2,
即一元二次不等式x2﹣4>0的解集为x>2或x<﹣2.
解答下列问题:
(1)一元二次不等式x2﹣25>0的解集为 ;
(2)分式不等式![]() 的解集为 ;
的解集为 ;
(3)解一元二次不等式2x2﹣3x<0.
【答案】(1)x>5或x<-5.(2)x>3或x<1;(3)0<x<![]()
【解析】试题分析:(1)将一元二次不等式的左边因式分解后化为两个一元一次不等式组求解即可;(2)据分式不等式大于零可以得到其分子、分母同号,从而转化为两个一元一次不等式组求解即可;(3)将一元二次不等式的左边因式分解后化为两个一元一次不等式组求解即可.
试题解析:
(1)∵x2-25=(x+5)(x-5)
∴x2-25>0可化为
(x+5)(x-5)>0
由有理数的乘法法则“两数相乘,同号得正”,得
①![]() ,②
,②![]()
解不等式组①,得x>5,
解不等式组②,得x<-5,
∴(x+5)(x-5)>0的解集为x>5或x<-5,
即一元二次不等式x2-25>0的解集为x>5或x<-5.
(2)∵![]()
∴![]() 或
或![]()
解得:x>3或x<1
(3)∵2x2-3x=x(2x-3)
∴2x2-3x<0可化为x(2x-3)<0
由有理数的乘法法则“两数相乘,异号得负”,得
①![]() 或②
或②![]()
解不等式组①,得0<x<![]() ,
,
解不等式组②,无解,
∴不等式2x2-3x<0的解集为0<x<![]()

【题目】要从甲、乙两名同学中选出一名,代表班级参加射击比赛. 现将甲、乙两名同学参加射击训练的成绩绘制成下列两个统计图:
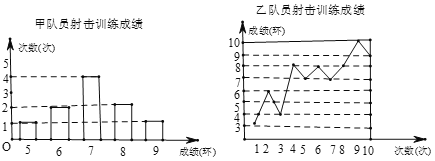
根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差( | |
甲 | 7 |
| 7 | 1. 2 |
乙 |
| 7. 5 |
| 4. 2 |
(1)分别求表格中![]() 、
、![]() 、
、![]() 的值.
的值.
(2)如果其他参赛选手的射击成绩都在7环左右,应该选______队员参赛更适合;如果其他参赛选手的射击成绩都在8环左右,应该选______队员参赛更适合.
【题目】某自行车厂一周计划生产150辆自行车,平均每天生产辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正、减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比生产量最少的一天多生产 辆;
(3)该厂实行计划工资制,每辆车![]() 元,超额完成任务每辆奖
元,超额完成任务每辆奖![]() 元,少生产一辆扣
元,少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?