Question

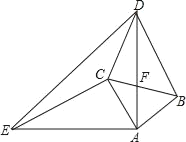
【题目】如图，△ABC和△ADE都是等腰直角三角形，AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°．

(1)求证：△ACE≌△ABD；

(2)若AC＝2，EC＝4，DC＝2，求∠ACD的度数；

(3)在(2)的条件下，直接写出DE的长为　 　．(只填结果，不用写计算过程)

Answer 1

【答案】(1)证明见解析；(2)∠ACD＝135°；(3)2.

【解析】

（1）根据等腰直角三角形的性质可以得出∠EAC=∠DAB，再有AB=AC，AD=AE，根据SAS就可以得出结论；

（2）根据勾股定理可以求出BC的值为2，就可以得出BC=DC，在△BCD中由勾股定理的逆定理可以得出△BCD为等腰直角三角形，就可以得出∠BCD=90°，从而得出∠ACD的度数；

（3）由（2）可以知道∠CDB=45°，而∠ABC=45°，就可以得出△ABD是直角三角形，由勾股定理就可以求出AB的值，再由勾股定理就可以求出DE的值．

解：(1)∵∠BAC＝∠DAE＝90°，

∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，

即∠EAC＝∠BAD．

在△ACE和△ABD中，

，

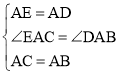∴△ACE≌△ABD(SAS)；

(2)∵△ACE≌△ABD(SAS)，

∴DB＝EC＝4，

在Rt△ABC中，AB2+AC2＝BC2，

∴BC2＝22+22＝8，

在△DBC中，BC2+DC2＝8+8＝16＝42＝BD2，

∴∠DCB＝90°，

∴∠ACD＝90°+45°＝135°；

(3)∵BC2＝8，DC2＝8，

∴BC＝DC．

∵∠DCB＝90°，

∴∠DBC＝45°．

∵∠ABC＝45°，

∴∠ABD＝90°．

在Rt△ABD中由勾股定理，得：

．

在Rt△AED中由勾股定理，得：

．

故答案为：．