题目内容
【题目】五一期间,甲、乙两人分别骑自行车和摩托车从![]() 地出发前往
地出发前往![]() 地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程
地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程![]() 与所用时间
与所用时间![]() 之间的函数图象如图所示.
之间的函数图象如图所示.

(1)甲骑自行车的速度是_____![]() .
.
(2)求乙休息后所行的路程![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
(3)为了保证及时联络,甲、乙两人在第一次相遇时约定此后两人之间的路程不超过![]() .甲、乙两人是否符合约定,并说明理由.
.甲、乙两人是否符合约定,并说明理由.
【答案】(1)0.25km/min;(2)![]() (50≤x≤110);(3)甲、乙两人符合约定.
(50≤x≤110);(3)甲、乙两人符合约定.
【解析】
(1)由图像可知,甲没有休息,匀速行驶,到终点时,行驶了30km,用了120min,即可求得其速度;
(2)首先根据图像可判定当甲走80min时,距A地20km,两人相遇,然后设乙休息后所行的路程y与x之间的函数关系为y=kx+b(k≠0),根据图像可得其经过(50,10)和(80,20)两点,列出二元一次方程组,解得即可,根据函数解析式,即可得出乙所用的时间,即得出自变量x的取值范围;
(3)根据图像信息,结合(1)和(2)的结论,判定当x=50,和x=110时,甲乙两人行驶的距离,判定两人距离差即可看是否符合约定.
解:(1)0.25km/min;
由图像可知,甲没有休息,匀速行驶,到终点时,行驶了30km,用了120min,其速度为
30÷120=0.25km/min;
(2)当甲走80min时,距A地20km,两人相遇.
设乙休息后所行的路程y与x之间的函数关系为y=kx+b(k≠0),
因为图像经过(50,10)和(80,20)两点,
由题意,得![]() ,
,
解得: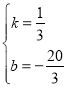 ,
,
所以y与x之间的函数关系式为![]() .
.
当y=30时,x=110.
所以自变量x的取值范围为50≤x≤110.
(3)当x=50时,甲走了12.5km,乙走了10km,12.5-10=2.5<3,符合约定.
当x=110时,甲走了27.5km,乙走了30km,30-27.5=2.5<3,符合约定.
所以甲、乙两人符合约定.

 天天向上口算本系列答案
天天向上口算本系列答案