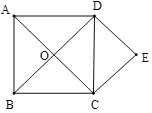
题目内容
【题目】在△BCF中,点D是边CF上的一点,过点D作AD∥BC,过点B作BA∥CD交AD于点A,点G是BC的中点,点E是线段AD上一点,且∠CDG=∠ABE=∠EBF.
(1)若∠F=60°,∠C=45°,BC=2![]() ,请求出AB的长;
,请求出AB的长;
(2)求证:CD=BF+DF.

【答案】(1)3+![]() (2)见解析
(2)见解析
【解析】
(1)过点E作EH⊥AB交AB于点H.分别求出AH,BH即可解决问题;
(2)连接EF,延长FE交AB与点M.想办法证明△BMF是等腰三角形即可解决问题;
解:(1)过点E作EH⊥AB交AB于点H.
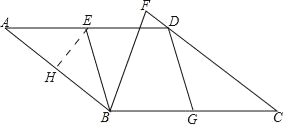
∵AD∥BC,AB∥CD,
∴四边形ABCD为平行四边形.
∴AB=DC,∠DAB=∠DBC,
在△CGD和△AEB中,
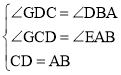 ,
,
∴△CGD≌△AEB,
∴∠DGC=∠BEA,
∴∠DGB=∠BED,
∵AD∥BC,
∴∠EDG+∠DGB=180°,
∴∠EDG+∠BED=180°
∴EB∥DG,
∴四边形BGDE为平行四边形,
∴BG=ED,
∵G是BD的中点,
∴BG=![]() BC,
BC,
∴BC=AD,ED=BG=![]() AD,
AD,
∵BC=2![]() ,
,
∴AE=![]() AD=
AD=![]() ,
,
在Rt△AEH中,∵∠EAB=45°,sin∠EAB=sin 45°=![]() ,
,
∴EH=![]() ,
,
∵∠EHA=90°,
∴△AHE为等腰直角三角形,
∴AH=EH=![]() ,
,
∵∠F=60°,
∴∠FBA=60°,
∵∠EBA=∠EBF,
∴∠EBA=30°,
在Rt△EHB中,tan∠EBH=tan 30°=![]() ,
,
∴HB=3,
∴AB=3+![]() .
.
(2)连接EF,延长FE交AB与点M.
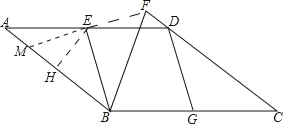
∵∠A=∠EDF,AE=DE,∠AEM=∠DEF,
∴△AEM≌△DEF(ASA),
∴DF=AM,ME=EF,
又∵∠EBA=∠EBF,
∴△MBF是等腰三角形
∴BF=BM,
又∵AB=AM+BM,
∴CD=BF+DF.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目