题目内容
点P(m,n)在反比例函数y=
(k≠0)的图象上,其中m,n是方程t2-4=0的两个根,则k的值是( )
| k |
| x |
| A、2或-2 | B、4或-4 |
| C、4 | D、-4 |
考点:反比例函数图象上点的坐标特征,解一元二次方程-直接开平方法
专题:
分析:先根据m,n是方程t2-4=0的两个根求出mn的值,再根据点P(m,n)在反比例函数y=
(k≠0)的图象上得出k的值即可.
| k |
| x |
解答:解:∵m,n是方程t2-4=0的两个根,
∴t2=4,解得t=±2,
∴m=2,n=-2或m=-2,n=2,
∵点P(m,n)在反比例函数y=
(k≠0)的图象上,
∴k=mn=2×(-2)=-4.
故选D.
∴t2=4,解得t=±2,
∴m=2,n=-2或m=-2,n=2,
∵点P(m,n)在反比例函数y=
| k |
| x |
∴k=mn=2×(-2)=-4.
故选D.
点评:本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
 如图是教学用直角三角板,边AC=30cm,∠C=90°,∠BAC=30°,则BC长为( )
如图是教学用直角三角板,边AC=30cm,∠C=90°,∠BAC=30°,则BC长为( )A、30
| ||
B、20
| ||
C、10
| ||
D、5
|
如图(1)是长方形纸带,∠DEF=α,将纸带沿EF折叠成图(2),再沿BF折叠成图(3),则图(3)中的∠CFE的度数是( )
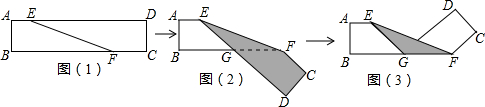

| A、2α |
| B、90°+2α |
| C、180°-2α |
| D、180°-3α |
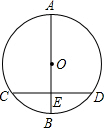 如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,CD=6cm,则直径AB=
如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,CD=6cm,则直径AB=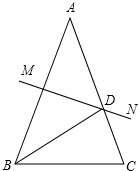 如图,在△ABC中,∠ABC=∠C,线段AB的垂直平分线MN交AC于点D.
如图,在△ABC中,∠ABC=∠C,线段AB的垂直平分线MN交AC于点D.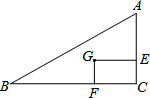 如图,点G是Rt△ABC的重心,过点G作矩形GECF,当GF:GE=1:2时,则∠B的正切值为
如图,点G是Rt△ABC的重心,过点G作矩形GECF,当GF:GE=1:2时,则∠B的正切值为