题目内容
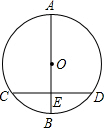 如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,CD=6cm,则直径AB=
如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,CD=6cm,则直径AB=考点:垂径定理,勾股定理
专题:
分析:连接OC,先根据垂径定理求出CE的长,设⊙O的半径为r,则OC=r,OE=
,在Rt△OCE中根据勾股定理即可求出r的值,故可得出结论.
| r |
| 2 |
解答: 解:连接OC,
解:连接OC,
∵AB⊥CD,CD=6cm,
∴CE=
CD=3cm,
设⊙O的半径为r,则OC=r,OE=
,
在Rt△OCE中,
OC2=OE2+CE2,即r2=32+(
)2,解得r=2
,
∴AB=2r=4
.
故答案为:4
.
 解:连接OC,
解:连接OC,∵AB⊥CD,CD=6cm,
∴CE=
| 1 |
| 2 |
设⊙O的半径为r,则OC=r,OE=
| r |
| 2 |
在Rt△OCE中,
OC2=OE2+CE2,即r2=32+(
| r |
| 2 |
| 3 |
∴AB=2r=4
| 3 |
故答案为:4
| 3 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
点P(m,n)在反比例函数y=
(k≠0)的图象上,其中m,n是方程t2-4=0的两个根,则k的值是( )
| k |
| x |
| A、2或-2 | B、4或-4 |
| C、4 | D、-4 |
下列计算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
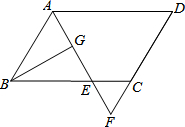 如图,在平行四边形ABCD中,AB=12,AD=18,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=
如图,在平行四边形ABCD中,AB=12,AD=18,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=