题目内容
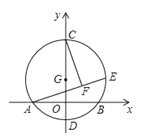
【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,BD=6,DC=4,求AD的长.小明同学利用翻折,巧妙地解答了此题,按小明的思路探究并解答下列问题:
(1)分别以AB,AC所在直线为对称轴,画出△ABD和△ACD的对称图形,点D的对称点分别为点E,F,延长EB和FC相交于点G,求证:四边形AEGF是正方形;
(2)设AD=x,建立关于x的方程模型,求出AD的长.

【答案】(1)证明见解析;(2)12.
【解析】
(1)先根据△ABD≌△ABE,△ACD≌△ACF,得出∠EAF=90![]() ;再根据对称的性质得到AE=AF,从而说明四边形AEGF是正方形;
;再根据对称的性质得到AE=AF,从而说明四边形AEGF是正方形;
(2)利用勾股定理,建立关于x的方程模型(x6)2+(x4)2=102,求出AD=x=12.
(1)证明:由题意可得:△ABD≌△ABE,△ACD≌△ACF,
∴∠DAB=∠EAB,∠DAC=∠FAC,又∠BAC=45![]() ,
,
∴∠EAF=90![]() .
.
又∵AD⊥BC,
∴∠E=∠ADB=90![]() ,∠F=∠ADC=90
,∠F=∠ADC=90![]() ,
,
∴四边形AEGF是矩形,
又∵AE=AD,AF=AD,
∴AE=AF,
∴矩形AEGF是正方形;
(2)解:设AD=x,则AE=EG=GF=x.
∵BD=6,DC=4,
∴BE=6,CF=4,
∴BG=x﹣6,CG=x﹣4,
在Rt△BGC中,BG2+CG2=BC2,
∴(x﹣6)2+(x﹣4)2=102.
化简得:x2﹣10x﹣24=0
解得:x1=12,x2=﹣2(舍去)
所以AD=x=12.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目