题目内容
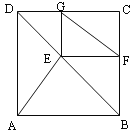
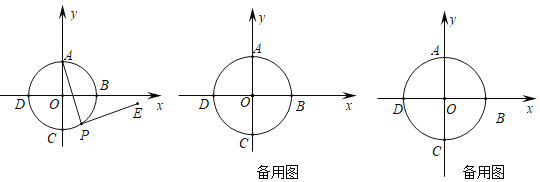
【题目】如图,AB为⊙O的直径,且AB=m(m为常数),点C为![]() 的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.
的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.
(1)当DC⊥AB时,则![]() = ;
= ;
(2)①当点D在![]() 上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;
上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;
②设CD长为t,求△ADB的面积S与t的函数关系式;
(3)当![]() 时,求
时,求![]() 的值.
的值.

【答案】(1)![]() ;(2)①DA+DB=
;(2)①DA+DB=![]() DC,②S=
DC,②S=![]() t2﹣
t2﹣![]() m2 ;(3)
m2 ;(3)![]() .
.
【解析】
(1)首先证明当DC⊥AB时,DC也为圆的直径,且△ADB为等腰直角三角形,即可求出结果;
(2)①分别过点A,B作CD的垂线,连接AC,BC,分别构造△ADM和△BDN两个等腰直角三形及△NBC和△MCA两个全等的三角形,容易证出线段DA,DB,DC之间的数量关系;
②通过完全平方公式(DA+DB)2=DA2+DB2+2DADB的变形及将已知条件AB=m代入即可求出结果;
(3)通过设特殊值法,设出PD的长度,再通过相似及面积法求出相关线段的长度,即可求出结果.
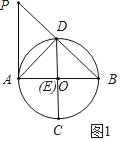
解:(1)如图1,∵AB为⊙O的直径,
∴∠ADB=90°,
∵C为![]() 的中点,
的中点,
∴![]() ,
,
∴∠ADC=∠BDC=45°,
∵DC⊥AB,
∴∠DEA=∠DEB=90°,
∴∠DAE=∠DBE=45°,
∴AE=BE,
∴点E与点O重合,
∴DC为⊙O的直径,
∴DC=AB,
在等腰直角三角形DAB中,
DA=DB=![]() AB,
AB,
∴DA+DB=![]() AB=
AB=![]() CD,
CD,
∴![]() =
=![]() ;
;
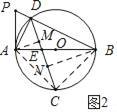
(2)①如图2,过点A作AM⊥DC于M,过点B作BN⊥CD于N,连接AC,BC,
由(1)知![]() ,
,
∴AC=BC,
∵AB为⊙O的直径,
∴∠ACB=∠BNC=∠CMA=90°,
∴∠NBC+∠BCN=90°,∠BCN+∠MCA=90°,
∴∠NBC=∠MCA,
在△NBC和△MCA中,
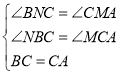 ,
,
∴△NBC≌△MCA(AAS),
∴CN=AM,
由(1)知∠DAE=∠DBE=45°,
AM=![]() DA,DN=
DA,DN=![]() DB,
DB,
∴DC=DN+NC=![]() DB+
DB+![]() DA=
DA=![]() (DB+DA),
(DB+DA),
即DA+DB=![]() DC;
DC;
②在Rt△DAB中,
DA2+DB2=AB2=m2,
∵(DA+DB)2=DA2+DB2+2DADB,
且由①知DA+DB=![]() DC=
DC=![]() t,
t,
∴(![]() t)2=m2+2DADB,
t)2=m2+2DADB,
∴DADB=t2﹣![]() m2,
m2,
∴S△ADB=![]() DADB=
DADB=![]() t2﹣
t2﹣![]() m2,
m2,
∴△ADB的面积S与t的函数关系式S=![]() t2﹣
t2﹣![]() m2;
m2;
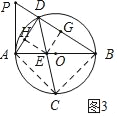
(3)如图3,过点E作EH⊥AD于H,EG⊥DB于G,
则NE=ME,四边形DHEG为正方形,
由(1)知![]() ,
,
∴AC=BC,
∴△ACB为等腰直角三角形,
∴AB=![]() AC,
AC,
∵![]() ,
,
设PD=9![]() ,则AC=20,AB=20
,则AC=20,AB=20![]() ,
,
∵∠DBA=∠DBA,∠PAB=∠ADB,
∴△ABD∽△PBA,
∴![]() ,
,
∴![]() ,
,
∴DB=16![]() ,
,
∴AD=![]() =12
=12![]() ,
,
设NE=ME=x,
∵S△ABD=![]() ADBD=
ADBD=![]() ADNE+
ADNE+![]() BDME,
BDME,
∴![]() ×12
×12![]() ×16
×16![]() =
=![]() ×12
×12![]() x+
x+![]() ×16
×16![]() x,
x,
∴x=![]() ,
,
∴DE=![]() HE=
HE=![]() x=
x=![]() ,
,
又∵AO=![]() AB=10
AB=10![]() ,
,
∴![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案