题目内容
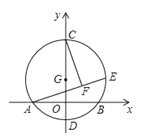
【题目】如图,以G(0,3)为圆心,半径为6的圆与x轴交于A.B两点,与y轴交于C,D两点,点E为⊙G上一动点,CF⊥AE于F,点E在⊙G的运动过程中,线段FG的长度的最小值为( )
A.![]() 1B.2
1B.2![]() -2C.3
-2C.3![]() D.3
D.3![]() 3
3
【答案】D
【解析】
如图,连接AC,作GM⊥AC,连接AG,由CF⊥AE于F可知,点F在以AC为直径的圆M上移动,当点F在MG的延长线上时,FG的长最小,根据含30°直角三角形的性质以及勾股定理求出MF,MG即可解答.
解:如图,连接AC,作GM⊥AC,连接AG,
∵GO⊥AB,
∴OA=OB
在Rt△AGO中,AG=6,OG=3,
∴AG=2OG,OA=![]() ,
,
∴∠GAO=30°,∠AGO=60°,
∵GC=GA=6,
∴∠ACG=∠CAG,
∵∠AGO=∠ACG+∠CAG,
∴∠ACG=∠CAG=30°,
∴AC=2AO=6![]() ,MG=
,MG=![]() ,
,
∴AM=3![]() ,
,
∵CF⊥AE于F,
∴点F在以AC为直径的圆M上移动,
当点F在MG的延长线上时,FG的长最小,最小值为FM-MG=3![]() -3,
-3,
故选:D.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目