题目内容
【题目】已知:如图1,抛物线的顶点为M:平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.
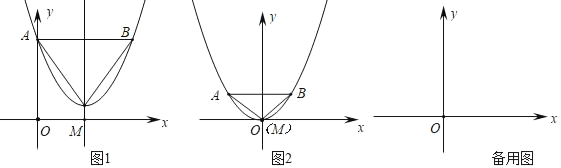
(1)如图2,求出抛物线y=x2的“完美三角形”斜边AB的长;
(2)若抛物线y=ax2+4的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线y=mx2+2x+n﹣5的“完美三角形”斜边长为n,且y=mx2+2x+n﹣5的最大值为﹣1,求m,n的值.
【答案】(1)2;(2)a=![]() 或﹣
或﹣![]() ;(3)m=﹣
;(3)m=﹣![]() ,n=
,n=![]()
【解析】
(1)设点B的坐标为:(m,m),把点B的坐标代入抛物线表达式得:m=m2,即可求解;
(2)①当a>0时,由(1)得:点B(m,m+4),AB=2m=4,则m=2,则点B(2,6),将点B的坐标代入抛物线表达式y=ax2+4即可求解;②当a<0时,设点B(m,4-m),同理可得:a=-![]() ,即可求解;
,即可求解;
(3)y=mx2+2x+n-5的最大值为-1,则抛物线开口向下,即m<0,设点B(s,-1-s),由mx2+2x+n-5的最大值为-1,则c-![]() =-1,即n-5-
=-1,即n-5-![]() …①,“完美三角形”斜边长为n,则2s=n…②,把点B的坐标代入抛物线表达式得:-1-s=ms2+2s+n-5…③,即可求解.
…①,“完美三角形”斜边长为n,则2s=n…②,把点B的坐标代入抛物线表达式得:-1-s=ms2+2s+n-5…③,即可求解.
(1)设点B的坐标为:(m,m),
把点B的坐标代入抛物线表达式得:m=m2,解得:m=0或1(舍去0),
故点B的坐标为:(1,1),则点A(﹣1,1),
则AB=2;
(2)①当a>0时,由(1)得:点B(m,m+4),
AB=2m=4,则m=2,则点B(2,6),
将点B的坐标代入抛物线表达式y=ax2+4得:
6=4a+4,解得:a=![]() ;
;
②当a<0时,设点B(m,4﹣m),
同理可得:a=﹣![]() ;
;
综上,a=![]() 或﹣
或﹣![]() ;
;
(3)y=mx2+2x+n﹣5的最大值为﹣1,则抛物线开口向下,即m<0,
设点B(s,﹣1﹣s),
由mx2+2x+n﹣5的最大值为﹣1,则c﹣![]() =﹣1,即n﹣5﹣
=﹣1,即n﹣5﹣![]() …①,
…①,
“完美三角形”斜边长为n,则2s=n…②,
把点B的坐标代入抛物线表达式得:﹣1﹣s=ms2+2s+n﹣5…③,
联立①②③并化简得:11s2﹣28s+16=0,解得:s=![]() (负值已舍去),
(负值已舍去),
m=﹣![]() ,n=
,n=![]() .
.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)的对应值如下表所示:
x | … | 0 |
| 4 | … |
y | … | 0.37 | -1 | 0.37 | … |
则方程ax2+bx+1.37=0的根是( )
A.0或4B.![]() 或
或![]() C.1或5D.无实根
C.1或5D.无实根