Question

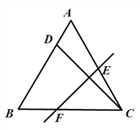
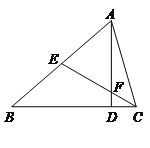
【题目】如图，在△ABC中，高AD与中线CE相交于点F，AD＝CE＝6，FD＝1，则AB＝______．

Answer 1

【答案】2

【解析】分析：过E作EG⊥BC于G，EH⊥AD于H，可以得出EG为AD的中位线，，进而得到∠ECD=30°，由30°角所对直角边等于斜边的一半，得到CF=2FD=2，得出EF的长，再由平行线的性质得到∠FEH=∠FCD=30°，从而得到HF，EH的长，进一步得到AH的长．在Rt△EHA中，由勾股定理得到AE的长，即可得到结论．

详解：过E作EG⊥BC于G，EH⊥AD于H．∵E为AB的中点，∴BE=AE．∵AD⊥BC，∴EG∥AD，∴BE：EA=BG：GD=1：1，∴EG为AD的中位线，，∴EG=AD==EC，∴∠ECD=30°，∴CF=2FD=2，∴EF=EC-FC=6-2=4．∵EG⊥AD，∴EH∥BC，∴∠FEH=∠FCD=30°，∴HF=EF=2，EH=HF=．∵AD=6，DF=1，HF=2，∴AH=6-1-2=3．在Rt△EHA中，AE===，∴AB=2AE=．故答案为：．