Question

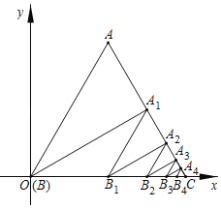
【题目】如图，等边三角形ABC的边长为4，顶点B与原点O重合，点C在x轴的正半轴上，过点B作BA1⊥AC于点A1，过点A1作A1B1∥OA，交OC于点B1；过点B1作B1A2⊥AC于点A2，过点A2作A2B2∥OA，交OC于点B2；……，按此规律进行下去，点A2020的纵坐标是_______

Answer 1

【答案】

【解析】

根据△ABC是等边三角形，得到AB=AC=BC=4，∠ABC=∠A=∠ACB=60°，解直角三角形得到A（2，），C（4，0），根据等腰三角形的性质得到AA1=A1C，根据中点坐标公式得到A1（3，），推出△A1B1C是等边三角形，得到A2是A1C的中点，求得A2（，），推出An（，），即可得到结论．

∵△ABC是等边三角形，

∴AB=AC=BC=4，∠ABC=∠A=∠ACB=60°，

∴A（2，），C（4，0），

∵BA1⊥AC，

∴AA1=A1C，

∴A1（3，），

∵A1B1∥OA，

∴∠A1B1C=∠ABC=60°，

∴△A1B1C是等边三角形，

∴A2是A1C的中点，

∴A2（，），

同理A3（，），

…

∴An（，）

∴A2020的纵坐标是，

故答案为：