题目内容
【题目】将连续的奇数1、3、5、7、9,……排成如下的数表:
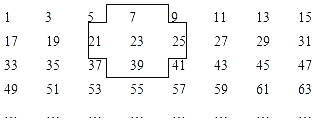
(1)十字框中的5个数的和与中间的数23有什么关系?若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗?
(2)设十字框中中间的数为a,用含a的式子表示十字框中的其他四个数;
(3)十字框中的5个数的和能等于2018吗?若能,请写出这5个数;若不能,说明理由.
【答案】(1)无论十字框如何平移,框住的5个数的和均为中间数的5倍;(2)a﹣16,a﹣2,a+2,a+16;(3)十字框中的5个数的和不能等于2018.
【解析】
(1)将5个数相加可得出十字框中的5个数的和为23的5倍,由数表排列的规律可得出:无论十字框如何平移,框住的5个数的和均为中间数的5倍;(2)设十字框中中间的数为a,根据所框数的特征,用含a的代数式表示出其它4个数即可求解;(3)假设成立,由(1)的结论可得出关于x的一元一次方程,解之即可求出x的值,由x的值不为整数可知假设不成立,进而可得出十字框中的5个数的和不能等于2018
(1)7+21+23+25+39=115=23×5,
∴十字框中的5个数的和为23的5倍.
无论十字框如何平移,框住的5个数的和均为中间数的5倍.
(2)设十字框中中间的数为a,则另外4个数分别为a﹣16,a﹣2,a+2,a+16.
(3)假设可以,设中间的数为x,
根据题意得:5x=2018,
解得:x=![]() .
.
∵![]() 不是整数,
不是整数,
∴假设不成立,
∴十字框中的5个数的和不能等于2018.

练习册系列答案
相关题目