Question

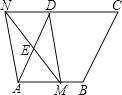
【题目】如图，在菱形ABCD中，AB=5，∠DAB=60°，点E是AD边的中点．点M是线段AB上的一个动点（不与点A重合），延长ME交射线CD于点N，连接MD、AN．

（1）求证：四边形AMDN是平行四边形；

（2）填空：①当AM的值为　　时，四边形AMDN是矩形；

②当AM的值为　　时，四边形AMDN是菱形。

Answer 1

【答案】（1）见解析（2）① ②5

【解析】

（1）四边形ABCD是菱形，则ND∥AM，故∠NDE=∠MAE，∠DNE=∠AME.由于E是AD边的中点，则DE=AE.由全等三角形的判定定理，得出△NDE≌△MAE，故ND=MA.

根据平行四边形的判定方法，即可得出四边形AMDN是平行四边形.

（1）证明：∵四边形ABCD是菱形，

∴ND∥AM，

∴∠NDE=∠MAE，∠DNE=∠AME，

又∵点E是AD边的中点，

∴DE=AE，

∴△NDE≌△MAE，

∴ND=MA，

∴四边形AMDN是平行四边形；

（2）解：① 若四边形AMDN是矩形，则∠DMA=90°，

在△AMD中，∠DMA=90°，∠DAB=60°，则∠ADM=30°.

在Rt△AMD中，∠AMD=30°，故AM=AD=.

②若四边形AMDN是菱形，则ADMN,

在Rt△MEA中，∠DAB=60°，则∠EMA=30°，

故AE=AM，即AM=2AE，

由于E是AD的中点，则AE=，

所以AM=2×=5.