题目内容
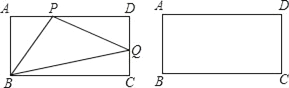
【题目】已知：如图，矩形ABCD中AB=4，AD=12，点P是线段AD上的一动点（点P不与点A，D重合），点Q是直线CD上的一点，且PQ⊥BP，连接BQ，设AP=x，DQ=y．
（1）求证：△ABP∽△DPQ．
（2）求y与x的函数关系式，并写出自变量x的取值范围．
（3）并求出当y取何值，△ABP∽△PBQ．
（4）若点Q在DC的延长线上，则x的取值范围 ．（不必写出过程）．
【答案】（1）见解析 （2）y=3x﹣
(0＜x＜12） （3）当y=9时．△ABP∽△PBQ （4）6﹣2
＜x＜6+2
【解析】分析：（1）根据四边形ABCD是矩形和PQ⊥BP，利用两组对应角相等即可求证△ABP∽△DPQ．
（2）根据△ABP∽△DPQ．利用其对应边成比例，将已知数值代入即可得出y与x的函数关系式．根据（点P不与点A，D重合），即可求出自变量x的取值范围．
（3）假设△ABP∽△PBQ．利用其对应边成比例，解得x的值，然后将x的值代入y=3x﹣即可．
（4）根据Q在DC的延长线上可知y＞4，即3x﹣
＞4，解此方程即可得出则x的取值范围．
详解：（1）∵四边形ABCD是矩形，∴∠A=∠D=90°，
∴∠ABP+∠APB=90°，∠PQD+∠QPD=90°．
∵PQ⊥BP，∴∠DPQ+∠APB=90°
∴∠APB=∠PQD，∴△ABP∽△DPQ；
（2）∵△ABP∽△DPQ，∴
=
．
∵AB=4，AD=12
∴
=
，即y=3x﹣．
∵AP与AD不重合，∴0＜x＜12；
答：y与x的函数关系式为：y=3x﹣；
自变量x的取值范围是：0＜x＜12；
（3）假设△ABP∽△PBQ，则
=
，即
=
，
将y=3x﹣
代入上式，解得：x=6．
将x=6代入y=3x﹣，解得：y=9．
答：当y=9时，△ABP∽△PBQ；
（4）∵Q在DC的延长线上，∴y＞4，即3x﹣＞4，解此方程得6﹣2＜x＜6+2．
故答案为：6﹣2＜x＜6+2．
