题目内容
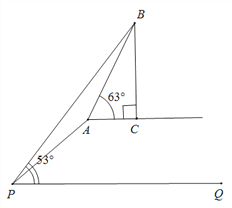
【题目】如图,坡度为1:2的斜坡AP的坡顶有一铁塔BC,在坡底P处测得塔顶B的仰角为53°,在沿斜坡前进![]() 米至A处,测得塔顶B的仰角为63°,已知A、C在同一水平面上.求铁塔BC的高度.
米至A处,测得塔顶B的仰角为63°,已知A、C在同一水平面上.求铁塔BC的高度.
(参考数据:sin63°≈0.89,cos63°≈0.45,tan63°≈2,sin53°≈0.8,cos53°≈0.6,tan53°≈![]() )
)
【答案】铁塔BC的高度约为25米
【解析】分析:作AD⊥PQ,垂足为D,延长BC交PQ于E,根据Rt△APD得出AD=5,PD=10,设BC的高度为x m,根据Rt△ACB的性质得出AC=![]() ,根据Rt△BPE的性质得出PE=
,根据Rt△BPE的性质得出PE=![]() ,然后根据PE-AC=10求出答案.
,然后根据PE-AC=10求出答案.
详解:解:作AD⊥PQ,垂足为D,延长BC交PQ于E,
在Rt△APD中AP=![]() ,坡度为1:2, 得AD=5,PD=10,
,坡度为1:2, 得AD=5,PD=10,
在矩形ADEC中,CE=AD=5,AC=DE,设BC的高度为x m,
在Rt△ACB中,tan63°=![]() , ∴AC=
, ∴AC=![]() ,
,
在Rt△BPE中,tan53°=![]() , ∴PE=
, ∴PE=![]() , ∴
, ∴![]() -
-![]() =10, 解得x=25.
=10, 解得x=25.
答:铁塔BC的高度约为25米

练习册系列答案
相关题目