题目内容
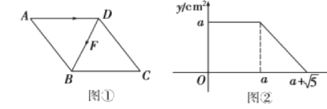
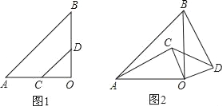
【题目】如图1、图2,△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90°,
(1)在图1中,AC与BD相等吗?请说明理由;
(2)若△COD绕点O顺时针旋转一定角度后,到达图2的位置,请问AC与BD还相等吗?为什么?
【答案】(1)相等;(2)相等
【解析】
(1)根据等腰三角形的两腰相等进行解答.
(2)证明△DOB≌△COA,根据全等三角形的对应边相等进行说明.
解:(1)相等.
在图1中,∵△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90°,
∴OA=OB,OC=OD,
∴0A﹣0C=0B﹣OD,
∴AC=BD;
(2)相等.
在图2中,∠AOB=∠COD=90°,
∵∠DOB=∠COD﹣∠COB,∠COA=∠AOB﹣∠COB,
∴∠DOB=∠COA
在△DOB和△COA中,
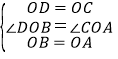 ,
,
∴△DOB≌△COA(SAS),
∴BD=AC.

练习册系列答案
相关题目