Question

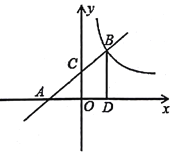
【题目】如图所示，点B的坐标为（0，4），点A是x正半轴上一点，点C在第一象限内，BC⊥AB于点B，∠OAB=∠BAC，当AC=10时，则过点C的反比例函数y=的比例系数k值为（　　）

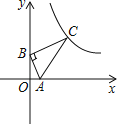
A.32 或 16B.48 或 64C.16 或 64D.32 或 80

Answer 1

【答案】C

【解析】

要确定k的值，只要求出点C的坐标即可，因此过点C作CDy轴，只要求出OD、CD即可，容易得到△AOB∽△BDC，又∠OAB=∠BAC，利用角平分线性质，可作BE⊥AC，构造全等三角形，得到OA=AE，CD=CE，又知AC=10，建立方程可求出点C的坐标，使问题得以解决．

解：过点C、B分别作CD⊥y轴，BE⊥AC，垂足为D、E，

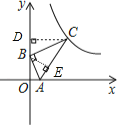
在△BOA和△BEA中，

∵∠OAB=∠BAC，AB=AB，∠BOA=∠BEA=90°，

∴△BOA≌△BEA，

∴BE=OB=4，OA=AE；

同理可证△CDB≌△CEB，

∴BD=BE=4，CD=CE；

∴OD=OB+BD=4+4=8，

易证△AOB∽△BDC，

∴，

设点C（m，8）

∴，

∴OA=

又∵AC=10，

∴AE+EC=10，

即：，

解得：m1=2，m2=8，

∴C（2，8）或C（8，8）

又∵点C在反比例函数y=的图象上，

∴k=2×8=16，或k=8×8=64，

故选：C．