题目内容
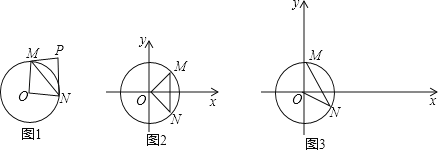
【题目】在平面直角坐标系中.抛物线y=﹣x2+4x+3与y轴交于点A,抛物线的对称轴与x轴交于点B,连接AB,将△OAB绕着点B顺时针旋转得到△O'A'B.
(1)用配方法求抛物线的对称轴并直接写出A,B两点的坐标;
(2)如图1,当点A'第一次落在抛物线上时,∠O'BO=n∠OAB,请直接写出n的值;
(3)如图2,当△OAB绕着点B顺时针旋转60°,直线A'O'交x轴于点M,求△A'MB的面积;
(4)在旋转过程中,连接OO',当∠O'OB=∠OAB时.直线A'O'的函数表达式是 .

【答案】(1)对称轴为x=2,A(0,3),B(2,0);(2)n=2;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)配方写成顶点式即可得到对称轴,从而求出B的坐标;
(2)利用抛物线的对称性易知△BFA′≌△BOA,从而推导出∠O'BO与∠OAB的关系;
(3)延长A'O'与x轴交于M,构造特殊的直角三角形,先求出MO′,再求△A′MB的面积;
(4)连接OO'与AB交于C,作O'E⊥x轴于E,可得△AOB∽△OEO′~△OCB,再利用对应边成比例可求出OC,O′E,OE,再求出A′O′的解析式.
(1)y=﹣x2+4x+3=﹣(x﹣2)2+7
所以对称轴为x=2,所以B(2,0)
当x=0时,y=3,
所以A(0,3);
(2)作A'F⊥x轴于F,由于二次函数的对称性,
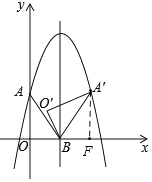
得OB=FB,AO=A'F
∵∠AOB=∠A'FB=90°,
∴△BFA'≌△BOA,设∠OAB=α,
则∠O′BO=180°(∠FBA′+∠O′BA′)=180°(90°-α+90°-α)=2α,
所以n=2;
(3)延长A'O'与x轴交于M,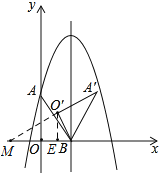
∵∠MBO′=60°,O′B=OB=2,
∴MO′=2![]()
∴S△A′MB=![]() (MO′+O′A′)O′B=2
(MO′+O′A′)O′B=2![]() +3;
+3;
(4)连接OO'与AB交于C,作O'E⊥x轴于E,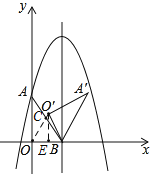
所以△AOB∽△OEO′~△OCB,
所以![]() ,
,
∴OC=![]() ,
,
同理可得:O′E=![]() ,OE=
,OE=![]() ,
,
所以O′(![]() ),B(2,0),
),B(2,0),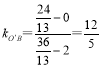 ,
,
所以kO′A′=![]() ,
,
所以A′O′:y=![]() x+3.
x+3.

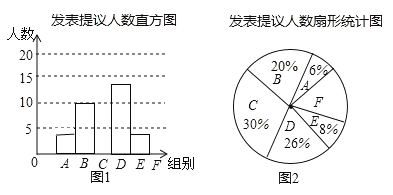
【题目】两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
(1)求得样本容量为 ,并补全直方图;
(2)如果会议期间组织1700名代表参会,请估计在这一天里发言次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.