题目内容
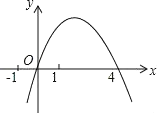
【题目】二次函数y=﹣x2+mx的图象如图，对称轴为直线x=2，若关于x的一元二次方程﹣x2+mx﹣t=0（t为实数）在1＜x＜5的范围内有解，则t的取值范围是（ ）
A.t＞﹣5B.﹣5＜t＜3C.3＜t≤4D.﹣5＜t≤4
【答案】D
【解析】
先根据对称轴x=2求得m的值，然后求得x=1和x=5时y的值，最后根据图形的特点，得出直线y=t在直线y=﹣5和直线y=4之间包括直线y=4．
∵抛物线的对称轴为x＝2，
∴
，m=4
如图，关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标
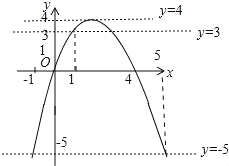
当x=1时，y=3，
当x=5时，y=﹣5，
由图象可知关于x的一元二次方程﹣x2+mx﹣t=0（t为实数）在1＜x＜5的范围内有解，
则直线y=t在直线y=﹣5和直线y=4之间包括直线y=4，
∴﹣5＜t≤4．
故选：D．
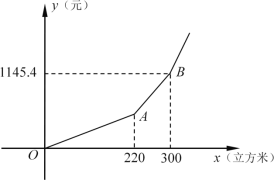
【题目】上海市为了增强居民的节水意识，避免水资源的浪费，全面实施居民“阶梯水价”．当累计水量达到年度阶梯水量分档基数临界点后，即开始实施阶梯价格计价，分档水量和价格见下表．
分档 | 户年用水量 （立方米） | 自来水价格 （元/立方米） | 污水处理费 （元/立方米） |
第一阶梯 | 0-220（含220） | 1.92 | 1.70 |
第二阶梯 | 220-300（含300） | 3.30 | 1.70 |
第三阶梯 | 300以上 | 4.30 | 1.70 |
注：1．应缴纳水费 = 自来水费总额 + 污水处理费总额 2．应缴纳污水处理费总额 = 用水量×污水处理费× 0.9 | |||
仔细阅读上述材料，请解答下面的问题，并把答案写在答题纸上：
（1）小静家2019年上半年共计用水量100立方米，应缴纳水费 元；
（2）小静家全年缴纳的水费共计1000.5元，那么2019年全年用水量为 立方米；
（3）如图所示是上海市“阶梯水价”y与用水量x的函数关系，那么第二阶梯（线段AB）的函数解析式为 ，定义域 ．
