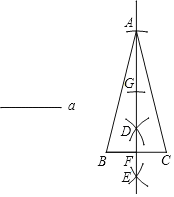题目内容
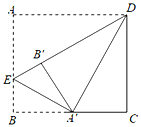
【题目】如图,在△ABC中,AB=AC,D为BC上一点(能与B重合,不与C重合),以DC为直径的半圆O,交AC于点E.
(1)如图1,若点D与点B重合,半圆交AB于点F,求证:AE=AF.
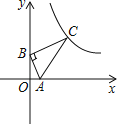
(2)设∠B=60°,若半圆与AB相切于点T,在图2中画出相应的图形,求∠AET的度数.
(3)设∠B=60°,BC=6,△ABC的外心为点P,若点P正好落在半圆与其直径组成的封闭图形的内部,直接写出DC的取值范围.

【答案】(1)证明见解析;(2)75°;(3)4<DC≤6.
【解析】
(1)连接BE,CF,根据已知条件,推断出△ABE≌△ACF即可;
(2)连接OT、OE、ET,根据已知推出∠OEC和∠TEO的度数,即可得出答案;
(3)以B为原点建立坐标系,求出各点坐标,设DC=a,写出圆O的解析式,再根据题意列出不等式计算即可.
证明:(1)如图1:连接BE,CF,

∵此时BC为直径,
∴∠BEC=∠CFB=90°,
∴∠AEB=∠AFC=90°,
又∵∠A=∠A,AB=AC,
∴△ABE≌△ACF,
∴AE=AF;
(2)如图2:连接OT、OE、ET,
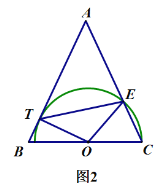
∵AB=AC,∠B=60°,
∴∠C=60°,
∵OE=OC,
∴∠EOC=∠OEC=60°,
∵AB是圆的切线,
∴OT⊥AB,
∵∠BOT=90°-60°=30°,
∴∠TOE=90°,
∵OT=OE,
∴∠TEO=45°,
∴∠AET=180°-45°-60°=75°;
(3)以B为原点建立坐标系,
∵AB=AC,∠ABC=60°,
∴△ABC为正三角形,
∵BC=6,
∴C(6,0),A(3,![]() ),
),
∴△ABC的外心P(3,![]() ),
),
设DC=a,则圆O:![]() ,
,
当P在封闭图形的内部时,![]() ,
,
得a>4,
∴4<DC≤6.

练习册系列答案
相关题目