题目内容
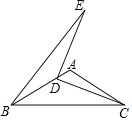
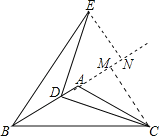
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,点D为AB边上一点(不与点B重合),连接CD,将线段CD绕点D逆时针旋转90°,点C的对应点为E,连接BE.若AB=2,则△BDE面积的最大值为_____.
【答案】![]()
【解析】
作CM⊥AB于M,EN⊥AB于N,根据AAS证得△EDN≌△DCM,得出EN=DM,然后解直角三角形求得AM=1,得到BM=3,设BD=x,则EN=DM=3﹣x,根据三角形面积公式得到S△BDE=![]() =
=![]() (3﹣x)=﹣
(3﹣x)=﹣![]() (x﹣1.5)2+
(x﹣1.5)2+![]() ,根据二次函数的性质即可求得.
,根据二次函数的性质即可求得.
解:作CM⊥AB于M,EN⊥AB于N,
∴∠EDN+∠DEN=90°,
∵∠EDC=90°,
∴∠EDN+∠CDM=90°,
∴∠DEN=∠CDM,
在△EDN和△DCM中
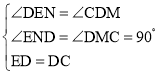
∴△EDN≌△DCM(AAS),
∴EN=DM,
∵∠BAC=120°,
∴∠MAC=60°,
∴∠ACM=30°,
∴AM=![]() AC=
AC=![]() 2=1,
2=1,
∴BM=AB+AM=2+1=3,
设BD=x,则EN=DM=3﹣x,
∴S△BDE=![]() =
=![]() (3﹣x)=﹣
(3﹣x)=﹣![]() (x﹣1.5)2+
(x﹣1.5)2+![]() ,
,
∴当BD=1.5时,S△BDE有最大值为![]() ,
,
故答案为![]() .
.

练习册系列答案
相关题目