��Ŀ����
����Ŀ���������P�ƶ���M��ת180�������Q�غϣ���ô�Ƶ�P���Q���ڵ�M�Գƣ�����M�����Գ����ģ���ʱ����M���߶�PQ���е㣮��ͼ����ֱ������ϵ�У���ABO�Ķ���A��B��O������ֱ�Ϊ��1��0������0��1������0��0��������P1��P2��P3�����е��������㶼������ABO��һ������Գƣ���P1���P2���ڵ�A�Գƣ���P2���P3���ڵ�B�Գƣ���P3���P4���ڵ�O�Գƣ���P4���P5���ڵ�A�Գƣ���P5���P6���ڵ�B�Գƣ���P6���P7���ڵ�O�Գƣ���������Щ�Գ���������ѭ������֪P1�������ǣ�1��1������P2019������Ϊ_____��
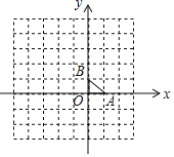
���𰸡�(-1,3)
��������
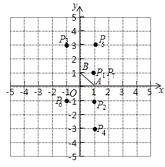
�����öԳ����ĵĶ���ֱ�ȷ��P1��P2��P3��P4��P5��P6��P7�����꣬���ֵ�P7������͵�P1��������ͬ������Щ���������6��Ϊһ�����ѭ�����ɴ˿�ȷ����P2019�����꣮
��ͼ�ߵ�P1�������ǣ�1��1����A��1��0����
����P1���P2���ڵ�A�Գƣ�
���P2��������1��1����
ͬ���õ���P3������Ϊ��1��3����
��P4��������1��3����
��P5��������1��3����
��P6��������1��1����
��P7��������1��1������
���P7������͵�P1��������ͬ��
��2019��336��6��3��
���P2019������͵�P3��������ͬ����Ϊ��1��3����
�ʴ��ǣ���1��3��.

 һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�