题目内容
【题目】抛物线y=![]() x2﹣3mx+2m+1与x轴正半轴交于A,B两点(A在B的左侧),与y轴正半轴交于点C,且OA=OC.
x2﹣3mx+2m+1与x轴正半轴交于A,B两点(A在B的左侧),与y轴正半轴交于点C,且OA=OC.
(1)抛物线的解析式为 (直接写出结果);
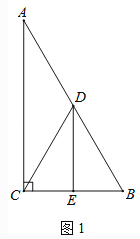
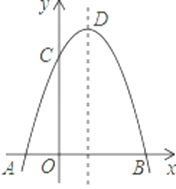
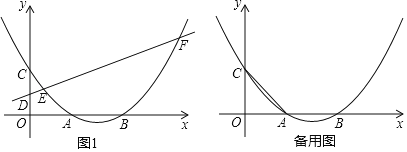
(2)如图1,D为y轴上一点,过点D的直线y=![]() x+n交抛物线于E,F,若EF=5
x+n交抛物线于E,F,若EF=5![]() ,求点D的坐标;
,求点D的坐标;
(3)将△AOC绕平面内某点逆时针旋转90°至△A'O'C'(点A,C,O的对应点分别为A',C',O'),若旋转后的△A'O'C'恰好有一边的两个端点落在抛物线上,请求出点A'的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x+2;(2)点D的坐标为:(0,
x+2;(2)点D的坐标为:(0,![]() );(3) 点A′的坐标为:(6,2)或(4,2).
);(3) 点A′的坐标为:(6,2)或(4,2).
【解析】
(1)点C(0,2m+1),OA=OC,则点A(2m+1),将点A的坐标代入抛物线的表达式,即可求解;
(2)联立①与直线EF的表达式并整理得:x2﹣8x+8﹣4n=0,则a+b=8,ab=8﹣4n,设直线EF的倾斜角为α,则tan![]() ,则cosα=
,则cosα=![]() ,则b﹣a=
,则b﹣a=![]() =2
=2![]() ,即可求解;
,即可求解;
(3)分A′C′在抛物线上、O′C′在抛物线上两种情况,分别求解即可.
解:(1)点C(0,2m+1),OA=OC,则点A(2m+1,0)
将点A的坐标代入抛物线的表达式并解得:m=![]() ,
,
故抛物线的表达式为:y=![]() (x2﹣6x+8)=
(x2﹣6x+8)=![]() x2﹣
x2﹣![]() x+2…①,
x+2…①,
故答案为:y=![]() x2﹣
x2﹣![]() x+2;
x+2;
(2)由抛物线的表达式知,点A、C的坐标分别为:(2,0)、(0,2),
则点D(0,n),设点E、F的纵坐标为:a,b,
联立①与直线EF的表达式并整理得:x2﹣8x+8﹣4n=0,
则a+b=8,ab=8﹣4n,
设直线EF的倾斜角为α,则tan![]() ,则cosα=
,则cosα=![]() ,
,
则b﹣a=![]() =2
=2![]() ,
,
(b﹣a)2=(a+b)2﹣4ab=64﹣4(8﹣4n)=(2![]() )2,解得:n=
)2,解得:n=![]() ,
,
故点D的坐标为:(0,![]() );
);
(3)将△AOC绕平面内某点逆时针旋转90°至△A'O'C'(点A,C,O的对应点分别为A',C',O'),
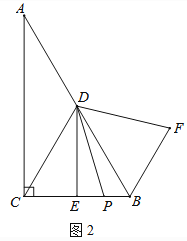
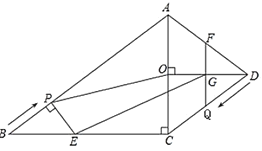
若旋转后的△A'O'C'恰好有一边的两个端点落在抛物线上,如图所示,
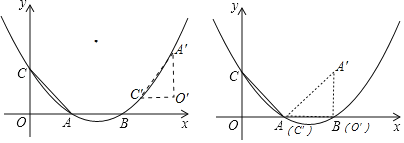
①当A′C′在抛物线上时(左侧图),
设点A′(x,y),则点C′(x﹣2,y﹣2),
将点A′、C′的坐标代入抛物线表达式得:
y=![]() (x2﹣6x+8),y﹣2=
(x2﹣6x+8),y﹣2=![]() [(x﹣2)2﹣6(x﹣2)+8)],
[(x﹣2)2﹣6(x﹣2)+8)],
解得:x=6,y=2,故点A′(6,2);
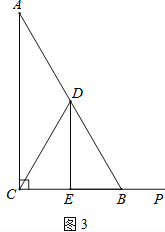
①当O′C′在抛物线上时(右侧图),A与C’重合,
由图象及旋转可得:OC=AB=2,OA=A’B=2
∴点A′(4,2);
综上,点A′的坐标为:(6,2)或(4,2).

 阅读快车系列答案
阅读快车系列答案