Question

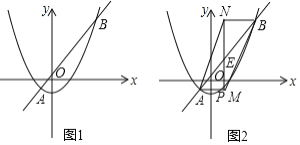
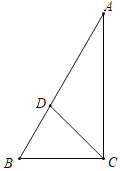
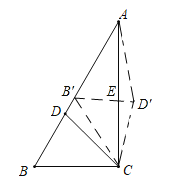
【题目】已知Rt△ABC中，∠ACB＝90°，∠B＝60°，BC＝4，D为AB边上一点，且BD＝3，将△BCD绕着点C顺时针旋转60°到△B′CD′，则AD′的长为_____．

Answer 1

【答案】

【解析】

取AB中点B′，连接B′D′交直线AC于点E，连接CB′，先证明△BCB′是等边三角形，即可证明△BCD≌△B′CD′，求出的长，即可求出AD′的长度.

解：取AB中点B′，连接B′D′交直线AC于点E，连接CB′，

在Rt△ABC中，∵∠ACB＝90°，∠B＝60°，BC＝4，

∴AB＝2BC＝8，AC＝BC＝4，

∵AB′＝B′B，

∴CB′＝BB′＝AB′，

∵∠B＝60°，

∴△BCB′是等边三角形，

∴CB′＝CB，∠BCB′＝60°，

∵CD＝CD′，∠DCD′＝60°，

∴∠BCB′＝∠DCD′，

∴∠BCD＝∠B′CD′，

∴△BCD≌△B′CD′（SAS），

∴BD＝B′D′＝3，∠B＝∠CB′D′＝60°，

∴∠CB′D′＝∠BCB′＝60°，

∴B′D′∥BC，

∵AB′＝B′B，

∴AE＝CE＝2，B′E＝BC＝2，

∴D′E＝B′D′﹣B′E＝3﹣2＝1，

在Rt△AED′中，AD′＝＝．

故答案为．