题目内容
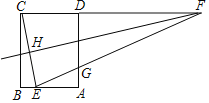
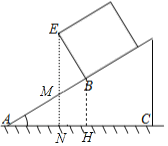
【题目】一个长方体木箱沿斜面下滑,当木箱下滑至如图所示位置时,AB=2m,已知木箱高BE=1m,斜面坡角为32°.(参考数据:sin32°=0.5299,cos32°=0.8480,tan32°=0.6249)
(1)求点B到AC的距离.(精确到0.1m)
(2)求木箱端点E距地面AC的高度.(精确到0.1m)

【答案】(1)点B到AC的距离为1.1m;(2)木箱端点E距地面AC的高度为1.9m
【解析】
(1)作BH⊥AC与H.根据sin32°=![]() 计算即可;
计算即可;
(2)作EN⊥AC与N交AB与M.分别求出EM、MN即可;
解:(1)作BH⊥AC与H.
∵sin32°=![]() ,
,
∴BH=2×0.5299≈1.1(m).
∴点B到AC的距离为1.1m.
(2)作EN⊥AC与N交AB与M.
在Rt△EMB中,∠MEM=32°,
∴EM=![]() ≈1.18(m),
≈1.18(m),
BM=EBtan32°≈0.62,
∴AM=AB﹣BM=0.38(m),
∴MN=AMsin32°≈0.73(m),
∴EN=EM+MN=1.18+0.73≈1.9(m).
∴木箱端点E距地面AC的高度为1.9m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目