题目内容
【题目】抛物线y=ax2+bx+3经过点A,B,C,已知A(-1,0),B(3,0).
(1)求抛物线的解析式;
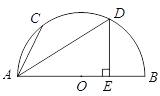
(2)如图1,P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,在(2)的条件下,延长DP交x轴于点F,M(m,0)是x轴上一动点,N 是线段DF上一点,当△BDC的面积最大时,若∠MNC=90°,请直接写出实数m的取值范围.

【答案】(1)抛物线的解析式为y=-x2+2 x+3;
(2)点P的坐标(![]() ,
, ![]() );
);
(3)实数m的取值范围是0≤m≤![]()
【解析】解:(1)由题意得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线解析式为y=-x2+2 x+3.
(2)在y=-x2+2 x+3中,当x=0,y=3,即C(0,3),
设直线BC的解析式为y=kx+b',则![]() 解得
解得![]()
∴直线BC的解析式为y=-x+3.
设P(x,3-x),则D(x,-x2+2 x+3)
∴S△BDC =S△PDC +S△PDB=![]() PD·x+
PD·x+![]() PD·(3-x)
PD·(3-x)
=![]() PD×3=
PD×3=![]() (-x2+3 x)
(-x2+3 x)
=![]() (x
(x![]() )2+
)2+![]() .
.
∴当x=![]() 时,△BDC的面积最大,
时,△BDC的面积最大,
此时P(![]() ,
, ![]() )
)
(3)0≤m≤![]()
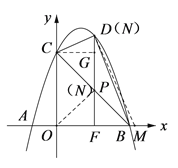 提示:将x=
提示:将x=![]() 代入y=-x2+2 x+3,得
代入y=-x2+2 x+3,得
y=,∴点D的坐标为(
![]() ,
, ![]() ),
),
过C点作CG⊥DF,则CG=![]() .
.
点N在DG上时,点N与点D重合时,
点M的横坐标最大.
∵∠ MNC=90°,∴![]() ,
,
∵C(0,3),D(![]() ,
, ![]() ),M(m,0),
),M(m,0),
∴![]()
![]() ,
,
解得m=![]() .即点M的坐标为(
.即点M的坐标为(![]() ,0),即m的最大值为
,0),即m的最大值为![]() ;
;
点N在线段GF上时,设GN=x,则NF=3-x,易证:Rt△NCG∽Rt△MNF,
∴![]() ,即
,即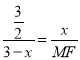 ,整理得,
,整理得,
MF=![]() =
=![]() ,∴当x=
,∴当x=![]() 时(N与P重合),MF有最大值
时(N与P重合),MF有最大值![]() ,
,
此时,M与O重合,∴M的坐标为(0,0),∴m的最小值为0,
故实数m的取值范围为0≤m≤![]() .
.